![[ ]
---ne(ψ-)--- -----p2------
fM (ψ,p) ≃ [2πT (ψ )]3∕2 exp - (1 + γ)Te (ψ)
e](NoticeDKE3458x.png)
Basically, the determination of the steady-state electron distribution function is an initial value problem, where the initial guess corresponds usually to the unperturbed solution of the linearized problem. For the zero-order Fokker-Planck equation, the Maxwellian distribution function is therefore by definition an eigenfunction of the collision operator, without external perturbation. Here the weakly relativistic solution corresponding to the condition on the relativistic factor γ - 1 ≪ 1 is considered at time t = 0,
![[ ]
---ne(ψ-)--- -----p2------
fM (ψ,p) ≃ [2πT (ψ )]3∕2 exp - (1 + γ)Te (ψ)
e](NoticeDKE3458x.png) | (5.398) |
where Te and ne
and ne are the electron temperature and density respectively. Details on the
notation are given in Sec. 6.3.1. Projected on the numerical grids, as defined in Sec.5.2, the
discrete form is
are the electron temperature and density respectively. Details on the
notation are given in Sec. 6.3.1. Projected on the numerical grids, as defined in Sec.5.2, the
discrete form is
![n [ p2 ]
fM,l+1∕2,i+1∕2,j+1∕2 ≃ [---e,l+1∕2]---exp - (------i+1∕)2------
2πTe,l+1∕2 3∕2 1+ γi+1∕2 Te,l+1∕2](NoticeDKE3461x.png) | (5.399) |
When the Lower Hybrid current drive problem is addressed, it is possible to start from a guess that already incorporate the existence of a plateau region, using the formulation given in Ref. [?] in the non-relativistic limit. When relativistic corrections must be considered, the effective perpendicular temperature T⊥ in the resonance domain must be usualy multipled by 2. Though this elegant approach seems attractive in order to reduce the total number of iterations for reaching the steady-state solution, its effectiveness is usualy poor when large time step Δt are considered. Indeed, the total number of time steps is merely determined by the relaxation time of the most energetic part of the fast electron tail prodiced by the wave. Since electrons are very weakly collisional, their relaxation time is very long as compared to the thermal one. Therefore, the gain for the rate of convergence is usually very small since the distribution model does not describe accurately the region above the plateau of the momentum space. Consequently, even if this method is implemented in the code, it is almost never used.
First order distribution function The initial distribution function for the first order drift kinetic equation is determined in the non-relativistic limit using the simplified Lorentz collision model corresponding to Zi ≫ 1 and Ti = 0, as introduced in Sec. 4.1.6. In that case, the bounce-averaged collision operator reduces to
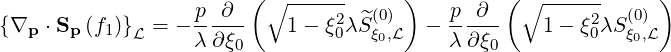 | (5.400) |
and in the steady-state regime 
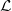 = 0 , so that the equation to be solved is
simply
= 0 , so that the equation to be solved is
simply
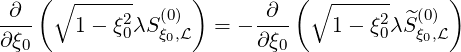 | (5.401) |
where
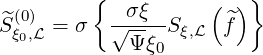 | (5.402) |
and
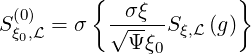 | (5.403) |
as defined in Sec.3.5.5.
Since only pitch-angle scattering takes place in this limit, 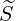 ξ0,
ξ0,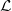 (0) may be expressed in a very
simple form
(0) may be expressed in a very
simple form
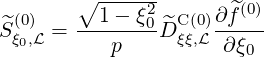 | (5.404) |
since FξC = DξpC = 0 for collisions with
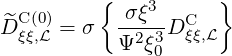 | (5.405) |
while
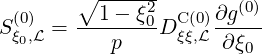 | (5.406) |
with
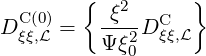 | (5.407) |
where Dξξ,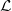 C = Bt
C = Bt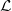 according usual notation given in Sec.4.1.6.
according usual notation given in Sec.4.1.6.
The differential equation to be solved is then
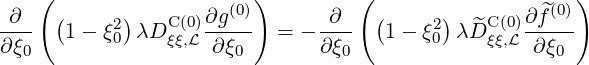 | (5.408) |
starting from the known expression of ∂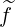 (0)∕∂ξ0. In the Lorentz limit, since Bt
(0)∕∂ξ0. In the Lorentz limit, since Bt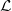 is simply
set to 1∕2, expressions of Dξξ,
is simply
set to 1∕2, expressions of Dξξ,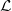 C(0) and
C(0) and 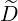 ξξ,
ξξ,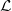 C(0) are obtained in a straightforward
manner,
C(0) are obtained in a straightforward
manner,
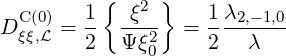 | (5.409) |
and
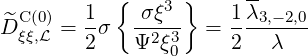 | (5.410) |
and g(0) is given by the simple equation
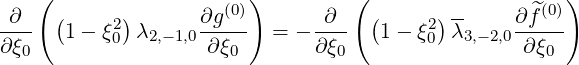 | (5.411) |
If the solution of the zero-order Fokker-Planck equation is the Maxwellian
![(0) ne [ p2 ]
f0 = fM ≃ -----3∕2 exp - ----
[2πTe ] 2Te](NoticeDKE3478x.png) | (5.412) |
its spatial derivative is
![(0) [ ( ) ]
∂f0-- = d-ln-ne + -p2-- 3- dlnTe- f
∂ψ dψ 2Te 2 dψ M](NoticeDKE3479x.png) | (5.413) |
and from the definition of 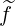 (0) given in Sec.3.4,
(0) given in Sec.3.4,
![(0) pξ0I (ψ)∂f (00)(ψ,p,ξ0)
f^ = -q-B--------∂ψ------
e 0 [ ( 2 ) ]
= pξ0I-(ψ)- dlnne-+ p---- 3- d-ln-Te fM (5.414)
qeB0 dψ 2Te 2 dψ](NoticeDKE3481x.png)
Projected on the numerical grids, the discrete form of 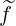 (0) is
(0) is
![p ξ I [d ln n ||
f^l(0+)1∕2,i+1∕2,j+1 ∕2 = -i+1∕2-0,j+1∕2-l+1∕2- -----e||
qeB0,l+1∕2 dψ l+1 ∕2
( p2 ) || ]
+ --i+1∕2--- 3- d-ln-Te|| fM,l+1∕2,i+1∕2,j+1∕2(5.415)
2Te,l+1∕2 2 dψ l+1∕2](NoticeDKE3483x.png)
Since fM is by definition independent of ξ0,
![[ ( ) ]
∂ ^f(0) pI-(ψ) dlnne- p2-- 3- d-ln-Te
∂ξ0 = qeB0 dψ + 2Te - 2 dψ fM
= Ξ (ψ,p)f (5.416)
M](NoticeDKE3484x.png)
![pI (ψ)[ dlnne ( p2 3) d ln Te]
Ξ(ψ,p ) =------ ------+ ----- -- ------
qeB0 dψ 2Te 2 dψ](NoticeDKE3485x.png) | (5.417) |
the equation becomes
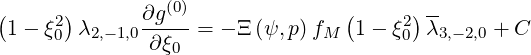 | (5.418) |
Assuming ∂g(0)∕∂ξ0 is finite at 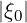 = 1, C = 0, and
= 1, C = 0, and
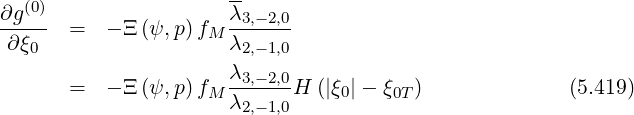
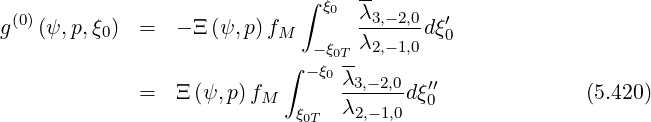
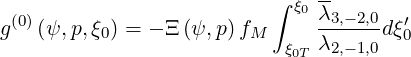 | (5.421) |
and gathering results
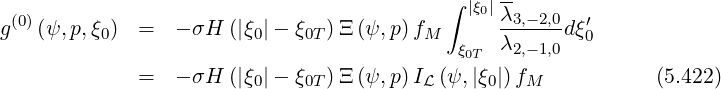
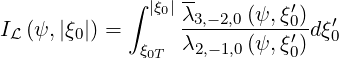 | (5.423) |
The discrete form of g(0)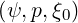 is
is
| gl+1∕2,i+1∕2,j+1∕2(0) | = -σ
j+1∕2H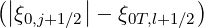 | ||
× Ξl+1∕2,i+1∕2I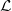 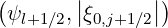 fM,l+1∕2,i+1∕2,j+1∕2 fM,l+1∕2,i+1∕2,j+1∕2 | (5.424) |
with
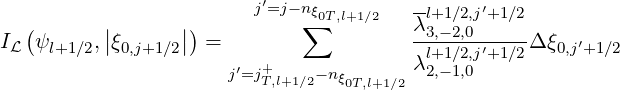 | (5.425) |
and j > jT,l+1∕2+.
Case of circular concentric flux surfaces According to Sec. 4.1.7,
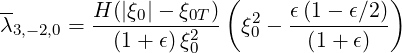 | (5.426) |
and Sec. 4.1.6
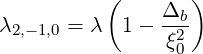 | (5.427) |
The integral I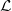
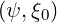 then becomes
then becomes
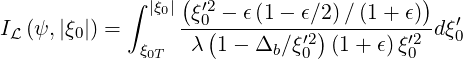 | (5.428) |
and in the low inverse aspect ratio limit ϵ ≪ 1, one finds
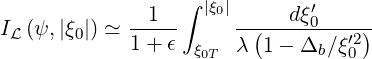 | (5.429) |
the expression that was first given in Ref. [?].
Flux surface averaged bootstrap current According to Sec. 3.6, the flux-averaged electron bootstrap current in the Lorentz model is given by the relation
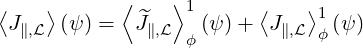 | (5.430) |
where
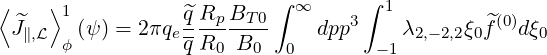 | (5.431) |
and
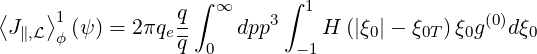 | (5.432) |
in the non-relativistic limit γ → 1. Therefore,
![⟨ ⟩1
^J∥,L (ψ) = 2 π^qRp-BT-0I (ψ)×
ϕ qR0 B20
∫ ∞ [dlnne ( p2 3 ) dlnTe] ∫ 1
------+ ----- -- ------ p4fM dp ξ20λ2,-2,2dξ0
0 dψ 2Te 2 dψ - 1
(5.433)](NoticeDKE3505x.png)
![⟨ ⟩1 q I (ψ) ∫ ∞ [d ln ne ( p2 3) d ln Te] 4
J∥,L ϕ (ψ ) = - 2πq--B---× --dψ-- + 2T-- 2- --dψ-- p fM dp
∫ 1 0 0 e
σH (|ξ |- ξ )ξ I (ψ, |ξ |)dξ (5.434)
-1 0 0T 0 L 0 0](NoticeDKE3506x.png)
Using relation R0BT0 = I , one obtains
, one obtains
![⟨ ^ ⟩1 ^qB2T0
J∥,L ϕ(ψ) = 2 πRp q-B20 ×
∫ ∞ [ ( 2 ) ] ∫ 1
dlnne-+ -p--- 3- dlnTe- p4fM dp ξ20λ2,-2,2dξ0
0 dψ 2Te 2 dψ - 1
(5.435)](NoticeDKE3508x.png)
![∫ ∞ [ ( 2 ) ]
⟨J ⟩1 (ψ) = - 2πq-R BT-0 × d-ln-ne + -p--- 3- dlnTe- p4f dp
∥,L ϕ q 0 B0 0 dψ 2Te 2 d ψ M
∫ 1
σH (|ξ0|- ξ0T)ξ0IL (ψ, |ξ0|)dξ0 (5.436)
-1](NoticeDKE3509x.png)
Since
![[ ( ) ] ( )
∫ ∞ d ln ne p2 3 dln Te 4 3 dlnne d ln Te
2π --dψ-- + 2T-- 2- --dψ-- p fM dp = 2neTe -dψ---+ --dψ--
0 e](NoticeDKE3510x.png) | (5.437) |
using the definite integral relation in Ref. [?],
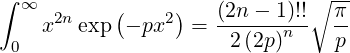 | (5.438) |
where  !! = 1.3.5... ×
!! = 1.3.5... × ,
,
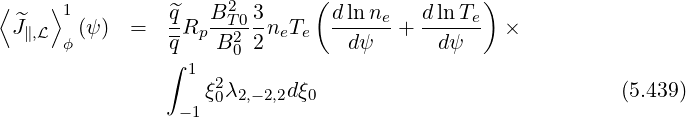
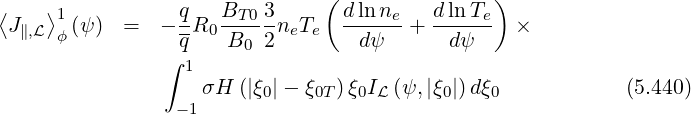
Finally,
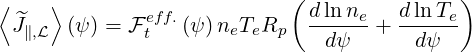 | (5.441) |
where the flux surface function usualy named “effective trapped fraction”  teff.
teff. is
is
![eff. 3-BT-0
F t (ψ ) = 2 B0 ×
[ ∫ 1 ∫ 1 ]
q^BT-0 ξ20λ2,-2,2dξ0 - q-R0 σH (|ξ0|- ξ0T) ξ0IL (ψ,|ξ0|)dξ0
q B0 - 1 q Rp -1
(5.442)](NoticeDKE3518x.png)
In the case of circular concentric flux surfaces,
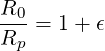 | (5.443) |
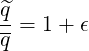 | (5.444) |
and
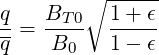 | (5.445) |
as shown in Sec. 3.6. Therefore,
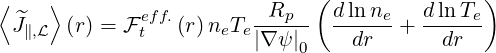 | (5.446) |
and using the relations R0BP0 = 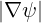 0, and R0BT0 = I
0, and R0BT0 = I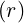 ,
,
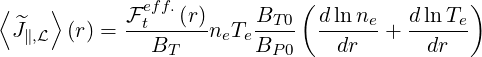 | (5.447) |
where RpBT = I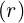 . Hence,
. Hence,
 teff. teff.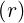 = =  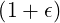 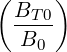 2 2 | |||
![[ ∫ 1 ∘ ----- ∫ 1 ]
ξ20λ2,0,0dξ0 - 1+-ϵ- σH (|ξ0|- ξ0T)ξ0IL (r,|ξ0|)d ξ0
-1 1- ϵ -1](NoticeDKE3531x.png) | |||
| (5.448) |
and since R0∕R = Ψ, λ2,-2,2 = λ2,0,0, as shown in Sec. 3.6. In the limit Bp ≪ BT , further simplifications may be carried out and
![[∫ ∘ -----∫ ]
eff. 3- 1 2 1-+-ϵ 1
lϵ→im0 F t (r) ≃ 2 (1 + ϵ) - 1ξ0λ2,0,0dξ0 - 1 - ϵ - 1σH (|ξ0|- ξ0T)ξ0IL(r,|ξ0|)dξ0](NoticeDKE3532x.png) | (5.449) |
The first term in the square bracket may be evaluated analyticaly. Indeed
![∫ 1 1 ∫ 1 [1 ∑ ] ∫ 2π dθ B ξ ξ2
ξ20λ2,0,0dξ0 = -- ξ20dξ0 -- ---ϵ----0-2
-1 ^q -1 2 σ T 0 2π BP ξξ0
∫ 1 [ ∑ ] ∫ 2π
= dξ0 1- d-θξ0ξ (5.450)
-1 2 σ T 0 2π](NoticeDKE3533x.png)
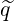 = ϵB∕BP . The sum over trapped electrons may be
dropped, since ξ0ξ is independent of σ. Therefore,
= ϵB∕BP . The sum over trapped electrons may be
dropped, since ξ0ξ is independent of σ. Therefore, 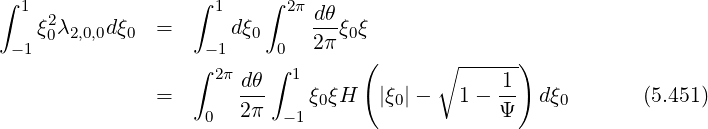
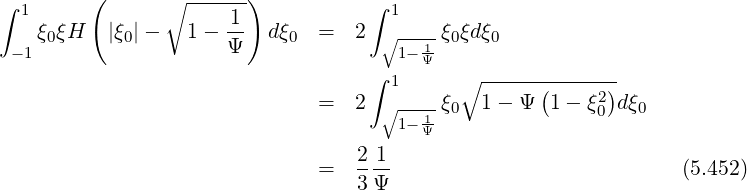
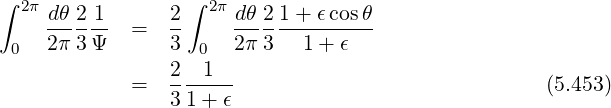
Consequently,
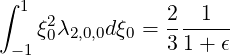 | (5.454) |
and using the
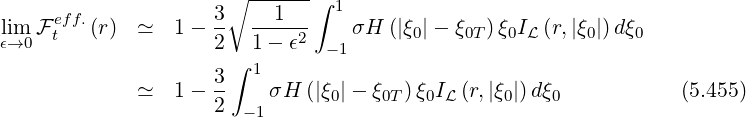
It can be shown in Appendix C after lengthly calculations, that
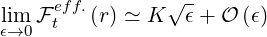 | (5.456) |
where
![√ -[ ]
3--2 ∑∞ ∑∞ ∞∑ ∑∞ -----------Ci1Ci2...Cim------------
K = 2 1 - ... 2i1+i2+...+im [2(i1 + i2 + ...+ im )- 1]
m i1 i2 im](NoticeDKE3541x.png) | (5.457) |
with
![2
Cn = -----[(2n-)!]-----
(2n - 1)23n (n!)4](NoticeDKE3542x.png) | (5.458) |
A rather fast convergence is obtained with m, and for m = n = 6, K ≃ 1.467, the usual value found in the litterature on neoclassical theory.