 if the small ϵ approximation
if the small ϵ approximation if the small ϵ approximation
if the small ϵ approximationWe can rewrite
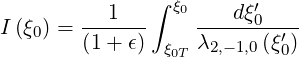 | (C.1) |
with, for ξ0′ > ξ0T ,
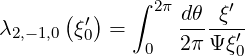 | (C.2) |
where
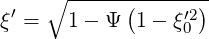 | (C.3) |
In the limit ϵ ≪ 1, we have
| Ψ | ≡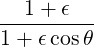 | ||
= 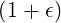 ![[ ( 2)]
1 - ϵcosθ + O ϵ](NoticeDKE5001x.png) | |||
= 1 + ϵ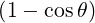 + + 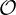 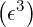 | (C.4) |
so that
| ξ′ | = ![∘ ----------------------------(------)
1 - [1+ ϵ(1 - cosθ)+ O (ϵ2)] 1- ξ′02](NoticeDKE5004x.png) | ||
= ξ0′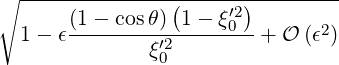 |
In fact, the series expansion of the square root must be kept to all orders for the term in ϵ, because the ratio ϵ∕ξ0′2 → 1 for ξ0′→ ξ0T . This gives
![{ ∞ [ ( ′2) ]n }
ξ′ = ξ′ 1 - ∑ ---(2n---2)!--- ϵ(1--cosθ)--1--ξ0-- + O (ϵ2)
0 22n- 1(n- 1)!n! ξ′20
n=1](NoticeDKE5006x.png)
where we used
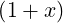 α α | = 1 + ∑
n=1∞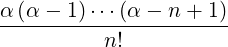 xn xn | (C.5) |
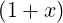 1∕2 1∕2 | = 1 + ∑
n=1∞ 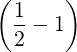  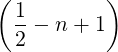 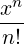 | (C.6) |
= 1 +  x + ∑
n=2∞ x + ∑
n=2∞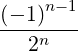 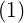 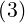  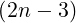 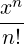 | (C.7) | |
= 1 +  x + ∑
n=2∞ x + ∑
n=2∞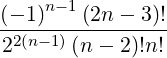 xn xn | (C.8) | |
= 1 + ∑
n=2∞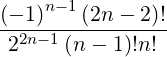 xn xn | (C.9) |
In addition,
 | = 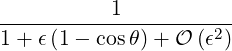 | ||
= 1 - ϵ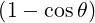 + + 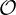 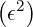 | (C.10) |
We get
λ2,-1,0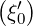 | = ∫
02π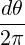 ![{ [ ] }
∞∑ (2n - 2)! ϵ(1- cosθ) (1- ξ′2) n
1 - ϵ(1- cosθ) - -2n-1---------- ---------′2------0--
n=12 (n- 1)!n! ξ0](NoticeDKE5031x.png) | (C.11) | |
= ∫
02π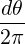 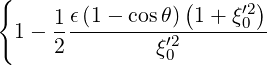 | |||
![∞ [ ( ′2)]n}
- ∑ ----(2n---2)!--- ϵ(1--cosθ-)-1--ξ0--
22n- 1(n- 1)!n! ξ′20
n=2](NoticeDKE5034x.png) | (C.12) | ||
= 1 -∑
n=1∞λ
2,-1,0(n) + +   | (C.13) |
with
λ2,-1,0(1)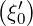 | = ∫
02π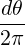 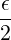 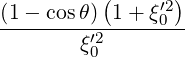 | (C.14) |
= 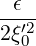 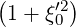 | (C.15) |
and, for n ≥ 2,
λ2,-1,0(n≥2)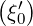 | = ∫
02π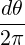 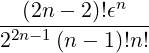 ![[ ]
(1- cosθ )(1- ξ′2)
---------′2-----0--
ξ0](NoticeDKE5046x.png) n n | (C.16) |
= 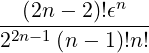 ![[ ]
(1- ξ′2)
----′20--
ξ0](NoticeDKE5048x.png) n ∫
02π n ∫
02π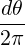 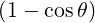 n n | (C.17) | |
= 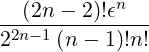 ![[ (1- ξ′2)]
----′20--
ξ0](NoticeDKE5052x.png) n ∫
02π n ∫
02π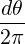 ![[ (θ )]
2 sin2 --
2](NoticeDKE5054x.png) n n | (C.18) | |
= 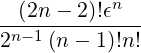 ![[(1 - ξ′2)]
----′2-0-
ξ0](NoticeDKE5056x.png) n ∫
0π n ∫
0π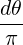 sin2nθ sin2nθ | (C.19) |
We can transform, for n ≥ 2,
| Y n | = ∫
0π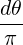 sin2nθ sin2nθ | ||
= ∫
0π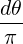 sinθ sin2n-1θ sinθ sin2n-1θ | |||
= 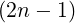 ∫
0π ∫
0π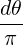 cos2θ sin2 cos2θ sin2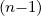 θ θ | |||
= 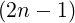 ![[∫ ∫ ]
πd-θsin2(n-1)θ - π dθsin2θ
0 π 0 π](NoticeDKE5064x.png) | |||
= 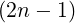 ![[Y n-1 - Y n]](NoticeDKE5066x.png) |
so that
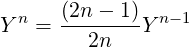
with
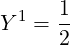
so that
| Y n | = 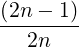 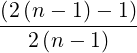  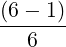 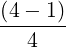  | ||
= ![(2n)!
----------------2
[2n(2n - 2)⋅⋅⋅2]](NoticeDKE5075x.png) | |||
= 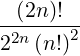 |
and we find
λ2,-1,0(n≥2) | = 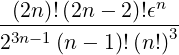 ![[ ]
(1- ξ′2)
---′20--
ξ0](NoticeDKE5079x.png) n n | (C.20) |
= ![[(2n)!]2 ϵn
---------------4
(2n - 1)23n (n!)](NoticeDKE5080x.png) ![[ ]
(1- ξ′2)
----′20--
ξ0](NoticeDKE5081x.png) n n | (C.21) |
We obtain
I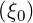 | = 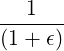 ∫
ξ0Tξ0 ∫
ξ0Tξ0
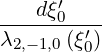 | ||
= 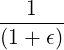 ∫
ξ0Tξ0
dξ0′ ∫
ξ0Tξ0
dξ0′![[ ∑∞ [∑∞ ( )]m ( )]
1+ λ(n2),-1,0 ξ′0 + O ϵ2
m=1 n=1](NoticeDKE5086x.png) | |||
= ∫
ξ0Tξ0
dξ0′![[ ∑∞ [ ∞∑ ]m ]
1- ϵ + λ(n) (ξ′) + O (ϵ2)
m=1 n=1 2,-1,0 0](NoticeDKE5087x.png) | |||
= ξ0 -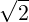 ϵ1∕2 + ∑
m=1∞I ϵ1∕2 + ∑
m=1∞I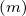 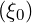 + + 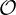 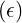 |
with
![[ ]m
∫ ξ0 ′ ∑∞ (n) ( ′)
I(m)(ξ0) = dξ0 λ2,-1,0 ξ0
ξ0T n=1](NoticeDKE5092x.png)
where we used
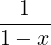 | = 1 + ∑ m=1∞xm | (C.22) |
| ξ0T | = 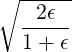 = = 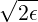 ![[ ϵ ( )]
1 - --+ O ϵ2
2](NoticeDKE5096x.png) | (C.23) |
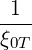 | = 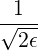 ![[ ]
1+ ϵ+ O (ϵ2)
2](NoticeDKE5099x.png) | (C.24) |
We have
![[ [( )]n ]m
∫ ξ0 ′ ϵ ( ′2) ∑∞ [(2n )!]2ϵn 1 - ξ′20
I(m )(ξ0) = dξ0 2ξ′2- 1+ ξ0 + ---------3n----4- ---ξ′2---
ξ0T 0 n=2 (2n- 1) 2 (n!) 0](NoticeDKE5100x.png)
Clearly, the only term of order ϵ-1∕2 comes from the ξ0′-2 contribution integrated and taken on ξ0T . We need to keep only
I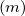 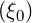 | = ∫
ξ0Tξ0
dξ0′![[ ∞ [ ]n]
∑ ---[(2n)!]2ϵn---- -1-
(2n- 1 )23n(n!)4 ξ′02
n=1](NoticeDKE5103x.png) m + m +   | ||
= ∫
ξ0Tξ0
dξ0′![[ [ ] ]
∑∞ n 1--n
ϵ Cn ξ′2
n=1 0](NoticeDKE5105x.png) m + m +   | |||
= ∫
ξ0Tξ0
dξ0′∑
i1=1∞∑
i2=1∞ ∑
im=1∞C
i1Ci2 ∑
im=1∞C
i1Ci2 Cimϵi1+i2+ Cimϵi1+i2+ +im +im
![[ ]
1--
ξ′20](NoticeDKE5110x.png) i1+i2+ i1+i2+ +im
+ +im
+   | |||
= ∑
i1=1∞∑
i2=1∞ ∑
im=1∞C
i1Ci2 ∑
im=1∞C
i1Ci2 Cimϵi1+i2+ Cimϵi1+i2+ +im
∫
ξ0Tξ0
dξ0′ +im
∫
ξ0Tξ0
dξ0′![[ 1 ]
-′2-
ξ0](NoticeDKE5116x.png) i1+i2+ i1+i2+ +im
+ +im
+   | |||
= ∑
i1=1∞∑
i2=1∞ ∑
im=1∞ ∑
im=1∞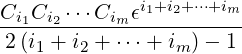 ![[ ]
- 1
-′2(i1+i2+-⋅⋅⋅+im)-1
ξ0](NoticeDKE5121x.png) ξ0Tξ0
+ ξ0Tξ0
+ 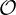 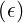 | |||
= 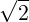 ϵ1∕2 ∑
i1=1∞∑
i2=1∞ ϵ1∕2 ∑
i1=1∞∑
i2=1∞ ∑
im=1∞ ∑
im=1∞![-----------Ci1Ci2 ⋅⋅⋅Cim-----------
2i1+i2+⋅⋅⋅+im [2(i1 + i2 + ⋅⋅⋅+ im) - 1]](NoticeDKE5125x.png) + + 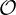 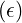 |
with
![2
C = -----[(2n-)!]-----
n (2n - 1)23n (n!)4](NoticeDKE5127x.png)
and finally we get
![√ -- [ ∑∞ ∑∞ ∑∞ ∑∞ ]
I (ξ0) = ξ0- 2ϵ1∕2 1- ⋅⋅⋅ -----------Ci1Ci2 ⋅⋅⋅Cim----------- +O (ϵ)
m=1 i1=1 i2=1 im=1 2i1+i2+⋅⋅⋅+im [2(i1 + i2 + ⋅⋅⋅+ im) - 1]](NoticeDKE5128x.png)
∫
-11dξ
0σξ0H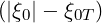 I I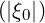 | |||
= 2∫
ξ0T1dξ
0ξ02 - ξ
0ϵ1∕2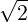 | |||
×![[ ∞ ∞ ∞ ∞ ]
1- ∑ ∑ ∑ ⋅⋅⋅∑ -----------Ci1Ci2 ⋅⋅⋅Cim-----------
2i1+i2+⋅⋅⋅+im [2(i1 + i2 + ⋅⋅⋅+ im )- 1]
m=1 i1=1i2=1 im=1](NoticeDKE5132x.png) + +   | |||
=  - ϵ1∕2 - ϵ1∕2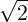 ![[ ]
∑∞ ∑∞ ∞∑ ∑∞ ------------Ci1Ci2-⋅⋅⋅Cim-----------
1 - ⋅⋅⋅ 2i1+i2+ ⋅⋅⋅+im [2 (i1 + i2 + ⋅⋅⋅+ im)- 1]
m=1 i1=1i2=1 im=1](NoticeDKE5136x.png) + +   |
and therefore
![|-----------------------------------------------------------------------------------|
| √ --[ ∞∑ ∑∞ ∑∞ ∑∞ ] ( ) |
K (ϵ) = 3--2 1- ⋅⋅⋅ -----------Ci1Ci2 ⋅⋅⋅Cim----------- + O ϵ1∕2 |
| 2 m=1 i1=1i2=1 im=1 2i1+i2+⋅⋅⋅+im [2(i1 + i2 + ⋅⋅⋅+ im )- 1] |
-------------------------------------------------------------------------------------](NoticeDKE5138x.png) | (C.25) |
with
![|----------------------|
| 2 |
|Cn = -----[(2n-)!]----4 |
------(2n---1)23n-(n!)--](NoticeDKE5139x.png)
For example, C1 = 1∕2, C2 = 3∕16, C3 = 5∕32, 
m | i1 | i2 | correction |
1 | 1 | - | 1∕4 |
1 | 2 | - | 1∕64 |
1 | 3 | - | 1∕256 |
1 | 4 | - | 25∕16384 |
1 | 5 | - | 17∕22737 |
2 | 1 | 1 | 1∕48 |
2 | 1 | 2 | 3∕1280 × 2 |
2 | 2 | 2 | 9∕28672 |
2 | 1 | 3 | 5∕7168 × 2 |
2 | 2 | 3 | 5∕49152 × 2 |
2 | 3 | 3 | 6∕173015 |
The sum of all these coefficient gives K = 1.486, which is already much better that
9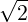 ∕8 = 1.591
∕8 = 1.591
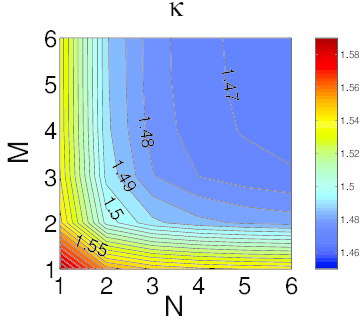
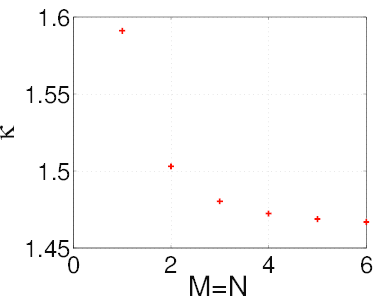
We compute the coefficient K for several values of the highest terms M and N in the series (C.25). The results are shown on Fig. C.1. We first see that K converges for high M and N, towards a value that seems close to 1.46. The best combination seems to be for M = N, as both high M and high N are needed for convergence. Therefore, we take M = N and calculate K as a function of M. Results are shown on Fig. C.2. We can see that K indeed converges, and that the asymptotic limit is about K = 1.46. For M = N = 6, we find K = 1.467.