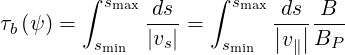
Normalized Expression The transit, or bounce time, is defined as the time for a passing particle to complete a full orbit in the poloidal plane, and for a trapped particle to complete half a bounce period. Note that this is possible only in the approximation of zero banana width. Otherwise, the bounce motion would be no longer symmetric in the forth and back motions, and both would need to be accounted for. We define then
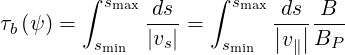 | (2.4) |
where vs is the guiding center velocity along the poloidal field lines, and v∥ is its velocity parallel to the magnetic field. B is the magnitude of the magnetic field, while BP is the magnitude of its poloidal component as shown in Fig. 2.5. The limits smin and smax are defined in (2.2) for passing electrons, and are the positions, along the field lines, of turning points for trapped electrons.
The differential arc length ds along the poloidal field line is generally expressed in curvilinear
coordinates 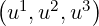 as (A.13)
as (A.13)
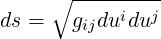 | (2.5) |
where the gij are the metric coefficients, defined in (A.12). In the 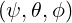 coordinates, the
variations dψ and dϕ are essentially zero along the poloidal field line. As a consequence, (2.5)
becomes
coordinates, the
variations dψ and dϕ are essentially zero along the poloidal field line. As a consequence, (2.5)
becomes
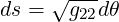 | (2.6) |
The velocity and momentum are related through the relativistic factor γ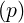 introduced in
Sec. 6.3.4, and therefore, we have
introduced in
Sec. 6.3.4, and therefore, we have
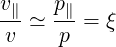 | (2.7) |
in the weak relativistic regime of tokamak plasmas, where the pitch-angle cosine ξ is defined in (A.247)
We get
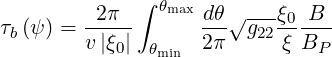 | (2.8) |
where ξ0 is the pitch angle cosine at the position θ0 of minimum B-field
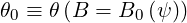 | (2.9) |
and the limits θmin and θmax will be calculated in the next subsection.
The bounce time can be normalized as such:
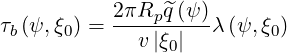 | (2.10) |
with
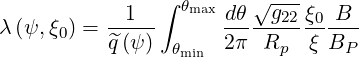 | (2.11) |
and
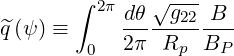 | (2.12) |
The bounce time is normalized to the transit time of particles with parallel momentum only,
such that λ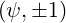 = 1.
= 1.
The covariant metric element g22 is given by (A.10)-(A.12), which is in the 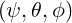 system
becomes (A.192)
system
becomes (A.192)
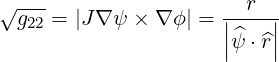 | (2.13) |
Consequently, the normalized bounce time takes the form
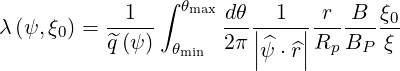 | (2.14) |
with
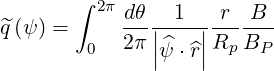 | (2.15) |
Particle Motion in the Magnetic Field The particle motion along the magnetic field lines exhibits one constant of the motion, the energy (or the total momentum p), and an adiabatic invariant, the magnetic moment μ. They are given by the equations
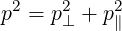 | (2.16) |
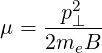 | (2.17) |
such that, as a function of the moment component 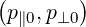 at the location θ0 of minimum
B-field, we have
at the location θ0 of minimum
B-field, we have
| p⊥2 + p ∥2 | = p ⊥02 + p ∥02 | (2.18) |
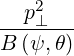 | = 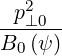 | (2.19) |
Using the transformation (A.250-A.251) from 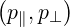 to
to 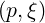 , the system (2.18-2.19)
becomes
, the system (2.18-2.19)
becomes
| p2 | = p 02 | (2.20) |
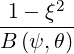 | = 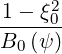 | (2.21) |
We get an expression for ξ as a function of ξ0:
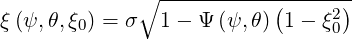 | (2.22) |
where σ = sign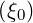 = sign
= sign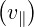 , and Ψ
, and Ψ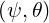 is the ratio of the total magnetic field B to its
minimum value B0
is the ratio of the total magnetic field B to its
minimum value B0
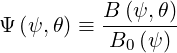 | (2.23) |
The trapping condition is given by 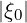 < ξ0T
< ξ0T 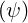 , where ξ0T
, where ξ0T 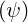 is the pitch angle, defined
at the minimum B0
is the pitch angle, defined
at the minimum B0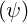 on a given flux-surface, such that the parallel velocity of the particle
vanishes at the maximum Bmax
on a given flux-surface, such that the parallel velocity of the particle
vanishes at the maximum Bmax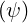 . An expression for ξ0T
. An expression for ξ0T 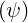 can then be obtained from (2.22):
setting ξ
can then be obtained from (2.22):
setting ξ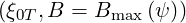 = 0, we get
= 0, we get
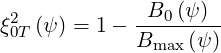 | (2.24) |
The turning points are
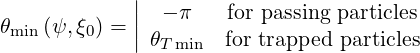 | (2.25) |
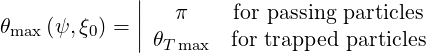 | (2.26) |
We can determine the turning angles θT min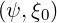 and θT max
and θT max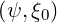 as the position where
ξ
as the position where
ξ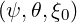 = 0. At this position, we have B = Bb
= 0. At this position, we have B = Bb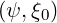 , where Bb
, where Bb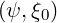 is then given by
(2.22)
is then given by
(2.22)
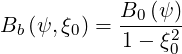 | (2.27) |
so that
θT min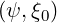 | = θ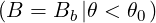 [2π] [2π] | (2.28) |
θT max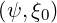 | = θ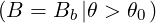 [2π] [2π] | (2.29) |
where θ0 is given by (2.9).
Calculation of λ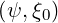 From the Output Data of Equilibrium Codes
The numerical calculation of λ
From the Output Data of Equilibrium Codes
The numerical calculation of λ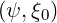 can be carried from the output of any magnetic
equilibrium code. In the kinetic code here considered, we use HELENA for magnetic flux surface
calculations [?], since it is used in the the CRONOS tokamak simulation package
[?].
can be carried from the output of any magnetic
equilibrium code. In the kinetic code here considered, we use HELENA for magnetic flux surface
calculations [?], since it is used in the the CRONOS tokamak simulation package
[?].
Data are assumed to be the parametrization of the flux-surfaces R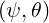 and Z
and Z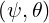 , and
the three components of the magnetic field BR
, and
the three components of the magnetic field BR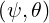 , BZ
, BZ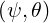 and Bϕ
and Bϕ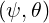 . From these
components we derive directly the toroidal and poloidal components of the field, as well as the
total field:
. From these
components we derive directly the toroidal and poloidal components of the field, as well as the
total field:
BT 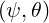 | = 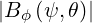 | ||
BP 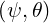 | = 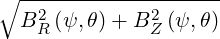 | ||
B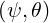 | = 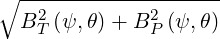 | (2.30) |
and also
| Rp | = R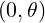 | (2.31) |
| Zp | = Z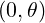 | (2.32) |
We also have an expression for r
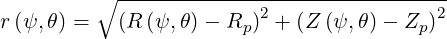 | (2.33) |
and, using relation
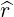 | = 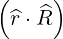 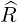 + + 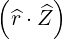 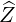 | ||
= 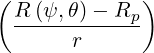 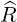 + + 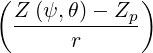 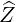 | (2.34) |
that can be easily deduced from vector relation in Fig. 2.2, we get an expression for the scalar product
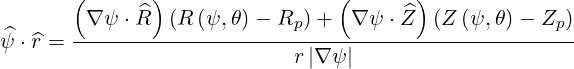 | (2.35) |
In a toroidal axisymmetric geometry, the magnetic field can be expressed generally as
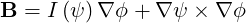 | (2.36) |
so that
| BT | = 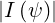 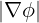 = = 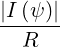 | (2.37) |
| BP | = 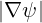 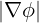 = = 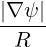 | (2.38) |
We also have
| BT | = I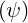 ∇ϕ = Bϕ ∇ϕ = Bϕ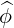 | (2.39) |
| BP | = ∇ψ ×∇ϕ = -BP 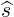 | (2.40) |
and therefore
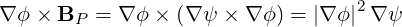 | (2.41) |
so that
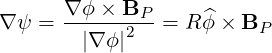 | (2.42) |
and we have the projections
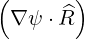 | = R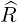 ⋅ ⋅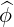 × BP = -RBZ × BP = -RBZ | (2.43) |
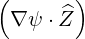 | = R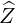 ⋅ ⋅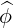 × BP = RBR × BP = RBR | (2.44) |
Finally, the expressions for the normalized bounce time λ and 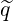 that are used in numerical
calculations are
that are used in numerical
calculations are
![[ ]
∫ θmax B (R - Rp)2 + (Z - Zp)2
λ (ψ,ξ0) = -1--- dθ-------------------------------ξ0-
^q(ψ) θmin 2π Rp |BR (Z - Zp )- BZ (R - Rp )| ξ](NoticeDKE123x.png) | (2.45) |
with
![∫ [ 2 2]
2πdθ---B--(R---Rp-)-+-(Z---Zp)-----
q^(ψ) = 0 2π Rp |BR (Z - Zp)- BZ (R - Rp )|](NoticeDKE124x.png) | (2.46) |
where R,Z,BR,BZ and B are functions of 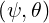 , and ξ is a function of
, and ξ is a function of 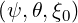 given by
(2.22).
given by
(2.22).
Safety Factor q The (averaged) safety factor q is defined in Ref. [?] in a general way as
The (averaged) safety factor q is defined in Ref. [?] in a general way as
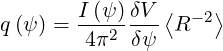 | (2.47) |
where V is the volume enclosed by a flux-surface and 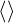 denotes the flux-surface
average.
denotes the flux-surface
average.
It can be expressed as
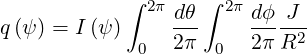 | (2.48) |
where the Jacobian J is given by (A.195)
| J | = 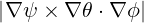 -1 -1 | ||
= 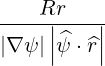 | |||
= 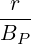 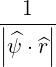 | (2.49) |
where (2.40) is used
We obtain
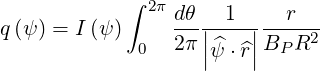 | (2.50) |
and, using (2.36), we finally have
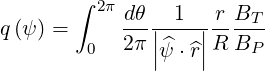 | (2.51) |
The expression of q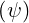 and its relation to
and its relation to 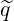
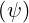 in the simplified case of circular concentric
flux-surfaces will be addressed in sub-section 2.2.2.
in the simplified case of circular concentric
flux-surfaces will be addressed in sub-section 2.2.2.
Using (2.33) and (2.35), we find the expression
![∫ [ 2 2]
2π dθ---(R----Rp)-+-(Z---Zp-)--BT--
q(ψ) = 2πR |BR (Z - Zp) - BZ (R - Rp)|
0](NoticeDKE140x.png) | (2.52) |
that is convenient for the numerical evaluation.
We are interested in calculating the toroidal extent of banana orbits, that is, the toroidal angle corresponding to the path done by a trapped particle between two turning points. It is given by
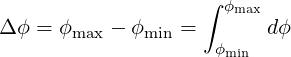 | (2.53) |
and can be expressed as a function of the length element dl along the path, using (A.198)
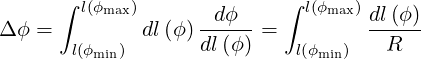 | (2.54) |
The poloidal and toroidal elements are related through the local angle of the magnetic field,
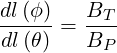 | (2.55) |
so that
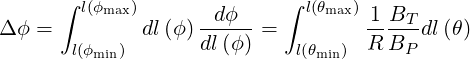 | (2.56) |
Using (A.197), we get
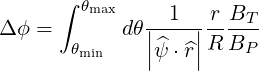 | (2.57) |
Defining the integral
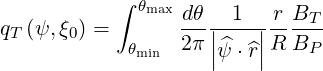 | (2.58) |
we find that the toroidal extent of banana orbits is
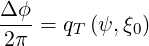 | (2.59) |
Note that at the trapped/passing limit, we have
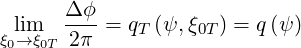 | (2.60) |
Therefore, we retrieve the interpretation of the safety factors, which is the number of toroidal rotations Δϕ∕2π for one poloidal rotation.
In order to reduce the dimension of kinetic equations, it is important to define an average over the poloidal motion, which anihilates the term that accounts for the time evolution of the variations of the distribution function along the field lines. The natural average is
![[ ∑ ] ∫ smax
{A } = 1- 1- -dsA
τb 2 σ T smin |vs|](NoticeDKE149x.png) | (2.61) |
where the sum over σ applies to trapped particles only.
It can be rewritten in terms of the normalized bounce time λ using expression (2.11)
![1 [ 1∑ ] ∫ θmax dθ√g--- B ξ
{A} = --- -- ------22----0 A
λ^q 2 σ T θmin 2π Rp BP ξ](NoticeDKE150x.png) | (2.62) |
or
![[ ] ∫
1-- 1∑ θmax dθ--1----r--B-ξ0
{A } = λ^q 2 2π||^ ||Rp BP ξ A
σ T θmin |ψ ⋅^r|](NoticeDKE151x.png) | (2.63) |
using relation (2.13).
Another expression uses the output data from equilibrium codes. Following the work in the previous section, we find
![[ ]
[ ] ∫ θ 2 2
{A } = 1-- 1-∑ max dθ---B--(R---Rp)-+-(Z---Zp-)----ξ0A
λ^q 2 θmin 2πRp |BR (Z - Zp) - BZ (R - Rp)| ξ
σ T](NoticeDKE152x.png) | (2.64) |
or explicitely
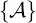 | = ![[ ]
⌊ ∫ θmax B (R - R )2 + (Z - Z )2 ⌋
⌈ dθ-------------p----------p-----ξ0⌉
θmin 2π Rp|BR (Z - Zp )- BZ (R - Rp )| ξ](NoticeDKE154x.png) -1× -1× | ||
![[ 1 ∑ ]
--
2 σ](NoticeDKE155x.png) T ∫
θminθmax T ∫
θminθmax
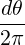 ![[ ]
B (R - Rp )2 + (Z - Zp)2
------------------------------
Rp |BR (Z - Zp)- BZ (R - Rp)|](NoticeDKE157x.png) 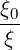 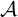 | (2.65) |
The bounce averaging of momentum-space operators in the kinetic equations leads to a set of coefficients that all have a similar structure, denoted λk,l,m and λk,l,m, which are define as
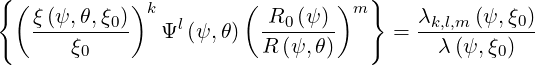 | (2.66) |
and
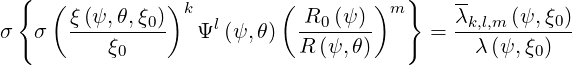 | (2.67) |
where
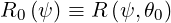 | (2.68) |
Note that by definition, λ0,0,0 = λ. In addition,
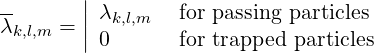 | (2.69) |
In this case, we have ψ = ψ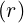 and therefore it is easier to work in the
and therefore it is easier to work in the 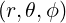 coordinate to
account for the symmetry in the problem. The normalized radius is
coordinate to
account for the symmetry in the problem. The normalized radius is
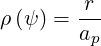 | (2.70) |
We have now
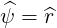 | (2.71) |
so that (A.113)
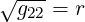 | (2.72) |
The toroidal field is
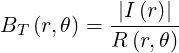 | (2.73) |
and the poloidal field is
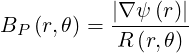 | (2.74) |
where
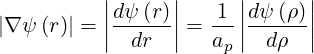 | (2.75) |
is now only a function of r or ρ.
The total field is then
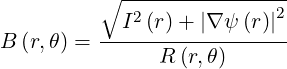 | (2.76) |
and can be written as
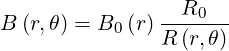 | (2.77) |
with
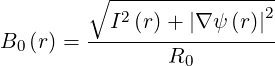 | (2.78) |
Consequently, we ratio of magnetic fields Ψ as defined in (2.23) becomes
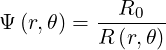 | (2.79) |
and
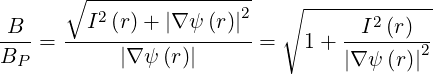 | (2.80) |
is a function of r only.
The safety factor given by expression (2.51) becomes
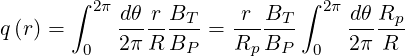 | (2.81) |
The averaged value of Rp∕R is evaluated in (??). It gives
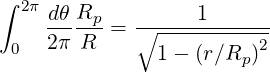 | (2.82) |
so that
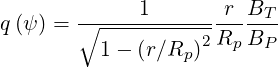 | (2.83) |
Note that in the factor 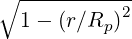 is usually neglected, which is valid only
in the large aspect ratio approximation, i.e. when the inverse aspect ratio ϵ defined
as
is usually neglected, which is valid only
in the large aspect ratio approximation, i.e. when the inverse aspect ratio ϵ defined
as
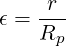 | (2.84) |
is much less than unity.
Using relation (A.95),
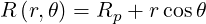 | (2.85) |
and recalling that the minimum B-field B0 corresponds to the poloidal angle value in that case
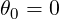 | (2.86) |
we find
Rmin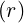 | = Rp - r = Rp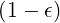 | (2.87) |
Rmax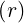 | = Rp + r = Rp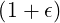 = R0 = R0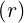 | (2.88) |
Therefore, the expression (2.79) becomes
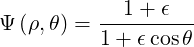 | (2.89) |
and using relation (2.77)
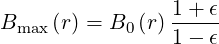 | (2.90) |
expression (2.24) is
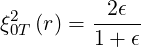 | (2.91) |
The pitch-angle cosine ξ is then given by combining relations (2.22 ) and (2.89)
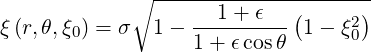 | (2.92) |
and the the turning angles are obtained from expression (2.27), or in the present notation
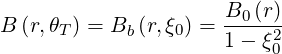 | (2.93) |
Using relation (2.89), one obtains
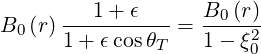 | (2.94) |
and then
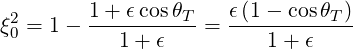 | (2.95) |
so that
![[ 2ξ2]
θT = arccos 1 - -20
ξ0T](NoticeDKE195x.png) | (2.96) |
and finally by symmetry
| θT min | = -θT | (2.97) | |
| θT max | = θT |
Using (2.72), the normalized bounce time reduces to
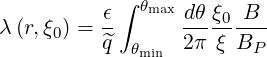 | (2.98) |
with, using definition (2.15)
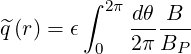 | (2.99) |
Because B∕BP only a function of r, as seen in (2.80), and can be taken out of the integrals, we get finally
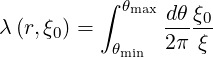 | (2.100) |
This integral can be performed analytically in a series expansion whose coefficients are
calculated in (??). Note that in the case where BT ≫ BP and in the large aspect ratio
approximation ϵ ≪ 1, we have 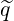
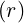 → q
→ q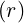 , which explains the notations, and the introduction
of pseudo safety factor like
, which explains the notations, and the introduction
of pseudo safety factor like 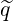 . Other new definitions of pseudo safety factors will be introduced
throughout the next sections, based on similar arguments.
. Other new definitions of pseudo safety factors will be introduced
throughout the next sections, based on similar arguments.