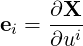
We consider the curvilinear coordinate system (u1,u2,u3).
The covariant, or tangent vector basis (e1,e2,e3)is defined as
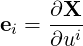 | (A.1) |
where the ei are tangent to the curvilinear lines. They can be normalized by
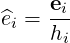 | (A.2) |
where we introduce the scale factors
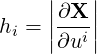 | (A.3) |
The gradient ∇f of a function f being defined by the differential
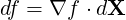 | (A.4) |
we apply to ui which gives
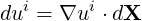 | (A.5) |
By chain rule, we have
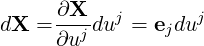 | (A.6) |
so that
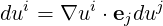 | (A.7) |
which implies
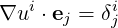 | (A.8) |
thus defining two reciprocal basis 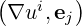 of vectors. The reciprocal basis vectors are also
called contravariant, and noted
of vectors. The reciprocal basis vectors are also
called contravariant, and noted
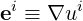 | (A.9) |
These vectors are perpendicular to the surfaces of constant ui.
From the properties of reciprocal basis, we can calculate a vector from the three vectors of the reciprocal basis, such that
| ei | = ∇ui = 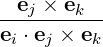 | (A.10) |
| ei | = 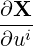 = = 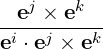 | (A.11) |
They are defined as
| gij | = ei ⋅ ej | (A.12) | |
| gij | = ei ⋅ ej |
With the differential vector given in (A.6), we show that the differential arc length along a curve is
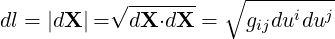 | (A.13) |
In addition, we have the relations
| ei | = gijej | (A.14) | |
| ei | = gije j |
We also show that
![[gij]](NoticeDKE4394x.png) | = ![[ ]
gij](NoticeDKE4395x.png) -1 -1 | (A.15) |
![[ ij]
g](NoticeDKE4396x.png) | = ![[gij]](NoticeDKE4397x.png) -1 -1 | (A.16) |
so that, defining
![g = det[gij]](NoticeDKE4398x.png) | (A.17) |
we find
![[ ]
g-1 = det gij](NoticeDKE4399x.png) | (A.18) |
We define the Jacobian
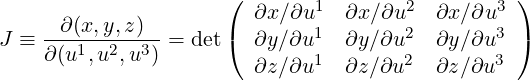 | (A.19) |
which gives
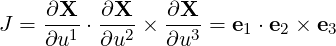 | (A.20) |
and the reciprocal Jacobian
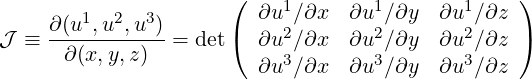 | (A.21) |
which gives
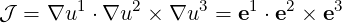 | (A.22) |
We can show that
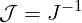 | (A.23) |
and the relations (A.10-A.11) become
| ei | =  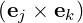 | (A.24) |
| ei | = J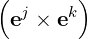 | (A.25) |
Also,
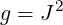 | (A.26) |
With
| A | = 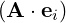 ei = A
iei ei = A
iei | (A.27) |
| A | = 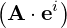 e
i = Aie
i e
i = Aie
i | (A.28) |
we find
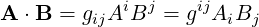 | (A.29) |
so that
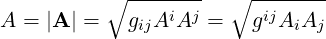 | (A.30) |
We also find
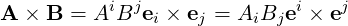 | (A.31) |
which gives
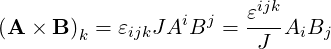 | (A.32) |
Note that from (A.14),
| Ai | = gijAj | (A.33) |
| Ai | = gijA j | (A.34) |
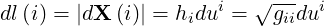 | (A.35) |
Equivalently,
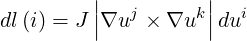 | (A.36) |
differential area in surface of constant ui Using
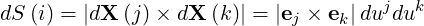 | (A.37) |
which becomes
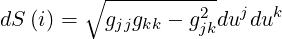 | (A.38) |
Equivalently
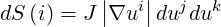 | (A.39) |
so that
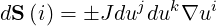 | (A.40) |
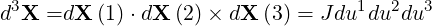 | (A.41) |
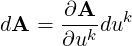 | (A.42) |
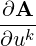 | = 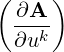 je
j ≡ Akje
j je
j ≡ Akje
j | (A.43) |
= 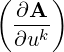 jej ≡ A
j,kej jej ≡ A
j,kej | (A.44) |
with
| Akj | = 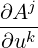 + Ai + Ai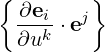 | (A.45) |
| Aj,k | = 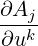 + Ai + Ai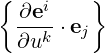 | (A.46) |
Then,
| δAj | = 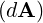 j = j = 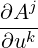 duk + Ai duk + Ai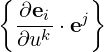 duk duk | (A.47) |
= dAj + 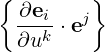 Aiduk Aiduk | (A.48) |
It can be shown that the Christoffel Symbol of the second kind is
![{ } { } [ ]
-∂ei⋅ej ≡ j = 1-gjn ∂gni + ∂gnk-- ∂gik
∂uk i k 2 ∂uk ∂ui ∂un](NoticeDKE4434x.png) | (A.49) |
so that
| Akj | = 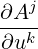 + + 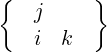 Ai Ai | (A.50) |
| Aj,k | = 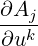 - -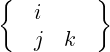 Ai Ai | (A.51) |
Note that since
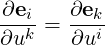 | (A.52) |
we have
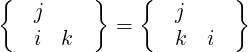 | (A.53) |
The operator ∇ can be decomposed in the curvilinear coordinates as
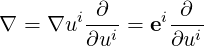 | (A.54) |
We then find the following differential operations:
Gradient It follows simply that
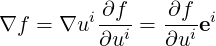 | (A.55) |
so that
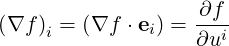 | (A.56) |
Divergence It can be shown that the divergence is expressed as
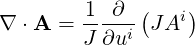 | (A.57) |
Curl It becomes, a compact notations,
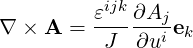 | (A.58) |
or is extended as
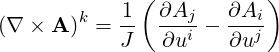 | (A.59) |