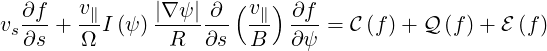
We recall the electron drift kinetic equation may be expressed as
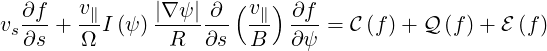 | (3.85) |
Each of these terms corresponds to a time evolution, and is therefore associated with a time-scale:
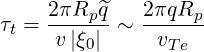 | (3.86) |
taking λ ~ 1 in that case, and q ≃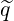 that is valid circular plasma cross-sections, and
v
that is valid circular plasma cross-sections, and
v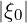 = v∥≃ vTe for thermal electrons. Since v∥≤
= v∥≃ vTe for thermal electrons. Since v∥≤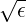 v
⊥ ≃
v
⊥ ≃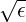 v
Te for trapped electrons, as
the consequence of the magnetic moment conservation, it turns out that τb may be
deduced directly from τt
v
Te for trapped electrons, as
the consequence of the magnetic moment conservation, it turns out that τb may be
deduced directly from τt
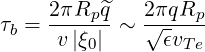 | (3.87) |
Consequently, τb ≥ τt, since ϵ ≤ 1, a result which is the consequence of the progressive slowing down of the parallel velocity as far as the electron approaches the turning point.
![∫ ψa Ωe R [ ∂ ( v∥)]- 1
τd = dψ ----------- --- --
0 v∥I (ψ)|∇ ψ| ∂s B](NoticeDKE310x.png) | (3.88) |
using expression 3.69 for the radial component vD ⋅∇ψ of the drift velocity vD as defined
in 3.59. Using relation I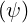 as defined in (2.37), and the fact that dψ∕
as defined in (2.37), and the fact that dψ∕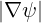 = dr for
circular concentric plasma cross-sections,
= dr for
circular concentric plasma cross-sections,
![Ωe ∫ ap dr [ ∂ ( 1) ]-1
τd ≃ -2-- B-- ∂s- B-
vTe 0 T](NoticeDKE313x.png) | (3.89) |
and since in that magnetic configuration ∂∕∂s ~ 2π∕Rp, ones obtains finally
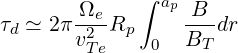 | (3.90) |
or
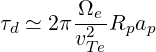 | (3.91) |
Consequently, the small drift parameter δd is defined as the ratio
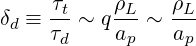 | (3.92) |
where the thermal Larmor radius ρL = vTe∕Ωe has been introduced.
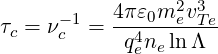 | (3.93) |
where lnΛ is the well known Coulomb logarithm, a slowly varying function of the plasma temperature and density. The collision time scale τc holds for circulating electrons.
For trapped ones, it is more physical to consider an alternate collision time scale determined not by the time for deflection of the path by π∕2, but by the time needed for the electron to be deflected so that it is no longer on a trapped orbit. In the limit ϵ ≪ 1, we can approximate the change of the pitch angle necessary to make trapped particles become untrapped
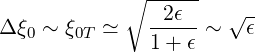 | (3.94) |
Because the small-angle collisions produce a random-walk change in the pitch-angle ξ0, the effective collision time for detrapping τceff. or τdt is approximately deduced from relation
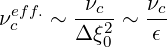 | (3.95) |
and
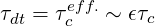 | (3.96) |
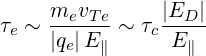 | (3.97) |
where the well known Dreicer field ED
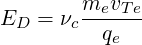 | (3.98) |
is introduced. Here only circulating particle are concerned.
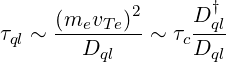 | (3.99) |
where Dql† = νc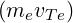 2.
2.
In the small drift expansion δd ≪ 1, where the small parameter is defined by relation (3.92)
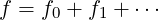 | (3.100) |
the first order equation is
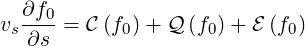 | (3.101) |
which is usually referred to as the Fokker-Planck equation.
The second order equation is
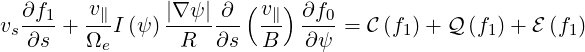 | (3.102) |
which is referred to as the electron Drift Kinetic equation.