7.3 Lower Hybrid Current drive
The Lower Hybrid current drive problem is one the more important addressed by
Fokker-Planck calculations in the field of fusion by magnetic confinement. It is also
certainly one of the most demanding case regarding the numerical constraints that must
be satisfied simultaneously such as possible discontinuities and large values of the
quasilinear diffusion coefficient, presence of cross-derivatives Dpξ = Dξp≠0. In that
conditions, the matrix conditionning may be significantly reduced, leading to possible
onset of numerical instabilities, lack of convergence or possible convergence towards
a solution that has no physical sense. In these conditions, the demonstration that
the code remains fully conservative and gives a physical solution for a domain of
parameters that is relevant for magnetic fusion simulations is a stringent test for
the validity of the projection technique of the kinetic equations on the numerical
grids as well as the correct description of both the internal and external boundary
conditions.
For the test procedure, a simplified expression of the quasilinear diffusion operator is
considered, as described in Appendix D.2.8, using the familiar boxcar shape in momentum space
D0,newLH = 1 for v1 ≤ v∥≤ v2, and D0,newLH = 0 otherwise, neglecting the factor vth†∕v∥, as
done usually in the litterature which only acceptable in principle when D0,newLH ≫ 1 (see Refs.
[?],[?],[?],[?]). For comparison with existing results, simulations are performed for the couples of
values 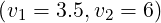 and
and 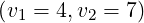 . Except it is specified, the default upper bound of
the integration domain is taken at pmax = 20. Plasma parameters are similar to those
used in Sec.7.1 dedicated to the the Ohmic conductivity problem, except that the
reference electron temperature may take two different values Te† = 5.11 × 10-4keV and
Te† = 5.11keV corresponding to non-relativistic to relativistic limits respectively. The choice of
these electron temperatures allows comparaison with already published results at
βth† = 0.01
. Except it is specified, the default upper bound of
the integration domain is taken at pmax = 20. Plasma parameters are similar to those
used in Sec.7.1 dedicated to the the Ohmic conductivity problem, except that the
reference electron temperature may take two different values Te† = 5.11 × 10-4keV and
Te† = 5.11keV corresponding to non-relativistic to relativistic limits respectively. The choice of
these electron temperatures allows comparaison with already published results at
βth† = 0.01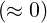 and βth† = 0.1. All corresponding plasma parameters are gathered
in section “CQL3D_LH” of the M-file “ptok_dke_1yp.m”, since it corresponds to
conditions that have been used for code comparison with the well known CQL3D code
[?].
and βth† = 0.1. All corresponding plasma parameters are gathered
in section “CQL3D_LH” of the M-file “ptok_dke_1yp.m”, since it corresponds to
conditions that have been used for code comparison with the well known CQL3D code
[?].
Concerning the numerical parameters, the code is running by default in the fully implicit
mode Δt = 10000, with the linearized electron-electron Belaiev-Budker collision operator that
conserve momentum. The drop tolerance for incomplete LU matrix factorization is 10-4, while
no Maxwellian solution is imposed at i = 1∕2. The momentum and pitch-angle grids are taken
uniform with np = nξ0 ≃ 200 except when simulations with different numbers of grid points or
non-uniform meshes are studied. Furthermore, no bounce averaging is considered, expect if
specified.
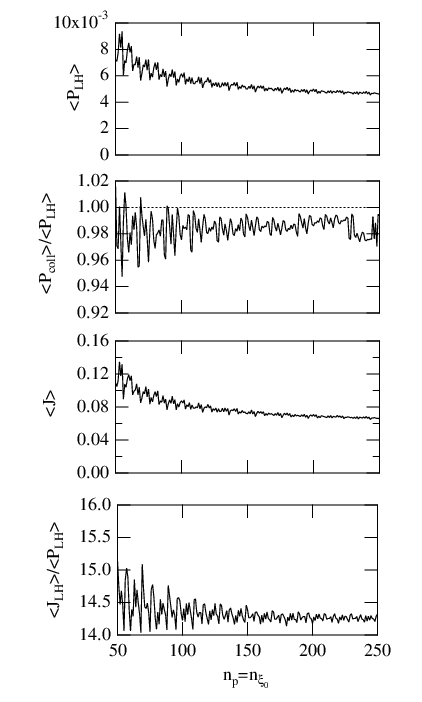
The first problem that is addressed is the numerical accuracy with the number of grid points.
For a pure hydrogen plasma 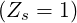 , np = nξ0 are varying from 50 to 250. Here a very simple
case is considered, with
, np = nξ0 are varying from 50 to 250. Here a very simple
case is considered, with 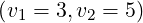 , using the relativistic Maxwellian collision operator, but
at βth† = 0.001 (non-relativistic limit). This allows easy comparison with previously
published results [?]. As shown in Fig.7.6, significant oscillations of the absorbed RF
, using the relativistic Maxwellian collision operator, but
at βth† = 0.001 (non-relativistic limit). This allows easy comparison with previously
published results [?]. As shown in Fig.7.6, significant oscillations of the absorbed RF
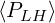 power density arises when
power density arises when 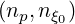 ≤ 150 which correspond to the relative
position of the lower bound of the Lower Hybrid resonance domain with respect to the
nearest grid point. The exponential decrease makes the solution very sensitive to this
parameter. For this domain of parameter, the power density absorbed by collisions
≤ 150 which correspond to the relative
position of the lower bound of the Lower Hybrid resonance domain with respect to the
nearest grid point. The exponential decrease makes the solution very sensitive to this
parameter. For this domain of parameter, the power density absorbed by collisions
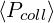 is not exactly equivalent to
is not exactly equivalent to 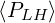 , though close to unity within 5%, leading to
oscillations of the ratio
, though close to unity within 5%, leading to
oscillations of the ratio 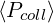 ∕
∕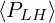 . The current density is clearly less sensitive to the
grid size, since it is mainly driven by the upper part of the tail. Nevertheless, small
oscillations are observed for a coarse grid. Consequently, the current drive efficiency is
varying significantly when
. The current density is clearly less sensitive to the
grid size, since it is mainly driven by the upper part of the tail. Nevertheless, small
oscillations are observed for a coarse grid. Consequently, the current drive efficiency is
varying significantly when 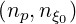 ≤ 150, as shown in Fig. 7.6, and a reltive accuracy
lower than 0.5% is only found when
≤ 150, as shown in Fig. 7.6, and a reltive accuracy
lower than 0.5% is only found when 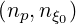 ≥ 150. From this systematic study, is
turns out that accurate calculations with uniform pitch-angle and momentum grids
require discrete steps lower than
≥ 150. From this systematic study, is
turns out that accurate calculations with uniform pitch-angle and momentum grids
require discrete steps lower than 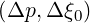 ≲ 0.13. The asymptotic value of the current
drive efficiency is found to reach 14.26, very close to the value 14.35 given in Ref. [?],
despite the fact that
≲ 0.13. The asymptotic value of the current
drive efficiency is found to reach 14.26, very close to the value 14.35 given in Ref. [?],
despite the fact that 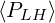 and
and 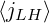 found by the code are larger by more than
10%. The difference arises likely from the collision operator that may exhibit some
differences.
found by the code are larger by more than
10%. The difference arises likely from the collision operator that may exhibit some
differences.
The effect of the grid size of memory storage requirements and the full elapsed time
for kinetic calculations. A shown in Fig.7.7 the memory used for data storage of  and
and 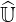 grows quadratically as expected from a 2 - D problem. The dashed line is a
parabolic fit that confirms this dependence. However, even if the scaling is quadratic,
memory requirement remains reasonable, because of the small coefficients pruning in the
matric factorization procedure. In the case here considered, the drop tolerance is fairly
low, 10-4, but large values may drastically reduce this size as discussed in Sec.6.2.1.
Much in the same way, the full elapsed time for kinetic calculations increases also
quadratically, but since time step is very large, is remains nevertheless lower than one
minute. This confirms the effectiveness of the code, which is fast, accurate and robust,
therefore fully designed for self-consistent realistic calculations that involve a chain of
codes.
grows quadratically as expected from a 2 - D problem. The dashed line is a
parabolic fit that confirms this dependence. However, even if the scaling is quadratic,
memory requirement remains reasonable, because of the small coefficients pruning in the
matric factorization procedure. In the case here considered, the drop tolerance is fairly
low, 10-4, but large values may drastically reduce this size as discussed in Sec.6.2.1.
Much in the same way, the full elapsed time for kinetic calculations increases also
quadratically, but since time step is very large, is remains nevertheless lower than one
minute. This confirms the effectiveness of the code, which is fast, accurate and robust,
therefore fully designed for self-consistent realistic calculations that involve a chain of
codes.
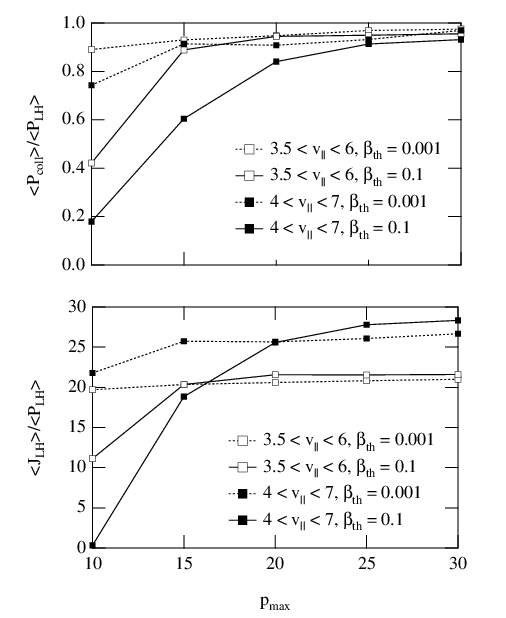
For a fixed number of grid points, the upper limit of the integration domain may have a
crucial role, especially when entering relativistic regimes at βth† = 0.1 and when the resonance
domain involves large values of v∥. As shown in Fig. 7.8 for a pure hydrogen plasma 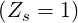 ,
pmax must be larger than 25 for
,
pmax must be larger than 25 for 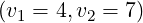 so that ηLH becomes independent of
pmax, while pmax ≃ 15 is acceptable for
so that ηLH becomes independent of
pmax, while pmax ≃ 15 is acceptable for 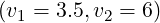 . The ratio between the
power absorbed by the Lower Hybrid wave and by collisions is also a good estimate of
the robustness of the calculations regarding this parameter. In principle, this ratio
must be close to unity, but significant departures are observed when the upper limit
of the integration domain in momentum space is too low. Consequently, for robust
estimate of the current drive efficiency in realistic tokamak simulations, pmax = 30 must
be considered as a reference value for relativistic calculations, providing the lower
bound of the resonance domain is larger than n∥≃ 1.4. As shown in Sec. 5.7.1, values
of n∥ lower than 1.4 becomes rapidly highly questionable when Te† exceeds 1keV ,
because of the relativistic curvature of the resonance domain that makes the code
fondamentaly non conservative, like in a runaway regime. Considering that in most
plasma conditions encountered in tokamaks, n∥ ≥ 1.4, the choice of pmax = 30 makes
the code fairly insensitive to the characteristics of the Lower Hybrid wave spectrum.
This is an important aspect for the robustness of self-consistent simulations. Since
the upper value of the momentum domain of integration is fairly large, the main
consequence is that the number of mometum or pitch-angle grid points must exceed
230.
. The ratio between the
power absorbed by the Lower Hybrid wave and by collisions is also a good estimate of
the robustness of the calculations regarding this parameter. In principle, this ratio
must be close to unity, but significant departures are observed when the upper limit
of the integration domain in momentum space is too low. Consequently, for robust
estimate of the current drive efficiency in realistic tokamak simulations, pmax = 30 must
be considered as a reference value for relativistic calculations, providing the lower
bound of the resonance domain is larger than n∥≃ 1.4. As shown in Sec. 5.7.1, values
of n∥ lower than 1.4 becomes rapidly highly questionable when Te† exceeds 1keV ,
because of the relativistic curvature of the resonance domain that makes the code
fondamentaly non conservative, like in a runaway regime. Considering that in most
plasma conditions encountered in tokamaks, n∥ ≥ 1.4, the choice of pmax = 30 makes
the code fairly insensitive to the characteristics of the Lower Hybrid wave spectrum.
This is an important aspect for the robustness of self-consistent simulations. Since
the upper value of the momentum domain of integration is fairly large, the main
consequence is that the number of mometum or pitch-angle grid points must exceed
230.
The physical benchmark of the code is performed by investigating the role played by
increasingly large values of Zs. Though this corresponds to unrealistic situations, it allows
interesting comparisons with theoretical results. As shown in Fig. 7.9, the current drive
efficiency defined as the ratio
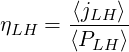 | (7.9) |
is decreasing as Zs rises as expected because of enhanced pitch-angle scattering, either for
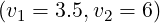 or
or 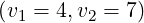 . Relativistic effects are almost negligible for the case
. Relativistic effects are almost negligible for the case
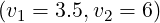 but also for
but also for 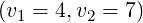 when the upper limit of the momentum
integration domain is pmax = 30. For pmax = 20, the current drive efficiency is significantly
underestimated, as discussed above, when large values of v∥ are considered, and when relativistic
effects become significant, i.e. when βth† = 0.1 in the case here considered. The current
drive efficiency scales roughly with the 1 - D non-relativistic model given in Ref.
[?]
when the upper limit of the momentum
integration domain is pmax = 30. For pmax = 20, the current drive efficiency is significantly
underestimated, as discussed above, when large values of v∥ are considered, and when relativistic
effects become significant, i.e. when βth† = 0.1 in the case here considered. The current
drive efficiency scales roughly with the 1 - D non-relativistic model given in Ref.
[?]
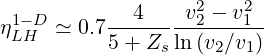 | (7.10) |
where the dependence 4∕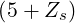 with Zs is deduced from Langevin analysis. It is found that
the coefficient 0.7 is independent of
with Zs is deduced from Langevin analysis. It is found that
the coefficient 0.7 is independent of 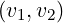 . This factor could arise from that fact that the
1 - D expression is obtained in the saturated limit corresponding to D0,newLH = +∞, while
numerical calculations are obtained with D0,newLH = 1. This result confirms on one
side the role played by pitch-angle scattering that make the kinetic problem a 2 - D
one, and that on the other side, important aspects of the 1 - D description remains
still valid. The 1 - D aspect of the Lower Hybrid physics is supported by the ratio
ηLH
. This factor could arise from that fact that the
1 - D expression is obtained in the saturated limit corresponding to D0,newLH = +∞, while
numerical calculations are obtained with D0,newLH = 1. This result confirms on one
side the role played by pitch-angle scattering that make the kinetic problem a 2 - D
one, and that on the other side, important aspects of the 1 - D description remains
still valid. The 1 - D aspect of the Lower Hybrid physics is supported by the ratio
ηLH![[v1 = 3.5,v2 = 6]](NoticeDKE4256x.png) ∕ηLH
∕ηLH![[v1 = 4,v2 = 7]](NoticeDKE4257x.png) which is close to the expected theoretical value 0.75
when Zs is not too large. In this regime, electron-electron interactions deeply contribute
to the current drive process that is fundamentaly 1-D in momentum space, since
resonace acceleration takes place along the magnetic field line. When Zs ≫ 1, the ratio
of current drive efficiencies drop much faster, since 2 - D effects start to become
important. From these tests, it is clear that the code captures most of the features of the
Lower Hybrid current drive. The parametric dependence with Zs indicates that 1 - D
physics predominates over the 2 - D one provided Zs is not too large. The 2 - D
effects are just corrections that may be incorporated in a single reduction factor. It
is important to mention that this result is independent of the model for describing
electron-ion collisions, considering an ion Maxwellian background, or the high-velocity
limit.
which is close to the expected theoretical value 0.75
when Zs is not too large. In this regime, electron-electron interactions deeply contribute
to the current drive process that is fundamentaly 1-D in momentum space, since
resonace acceleration takes place along the magnetic field line. When Zs ≫ 1, the ratio
of current drive efficiencies drop much faster, since 2 - D effects start to become
important. From these tests, it is clear that the code captures most of the features of the
Lower Hybrid current drive. The parametric dependence with Zs indicates that 1 - D
physics predominates over the 2 - D one provided Zs is not too large. The 2 - D
effects are just corrections that may be incorporated in a single reduction factor. It
is important to mention that this result is independent of the model for describing
electron-ion collisions, considering an ion Maxwellian background, or the high-velocity
limit.
Successful comparisons between different Fokker-Planck codes have been performed. Results
are given in Table 7.5 for a uniform grid,
Table 7.5: Lower Hybrid current drive efficiencies ηLH in a pure hydrogen plasma from
various 2 - D relativistic Fokker-Planck codes
considering the current efficiency in normalized units, but also an excellent agreement is
found in absolute units, as shown in Table 7.6
taking the same value for the Coulomb logarithm, lnΛ ≈ 15.
An important question is the code reliability owing to the increase of D0,newLH.
Indeed, in weak absorption regime, as often encountered in Lower Hybrid current
drive regime in present day tokamaks, D0,newLH may exceed significantly unity. In
principle, there is no limitation on the value of D0,newLH, and numerous analytical results
corresponds to the asymptotic solution D0,newLH = +∞. However, limitations do exist
in numerical simulations, and it is important to qualify the robustness of the code
regarding this problem. A systematic study has been performed for 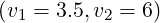 and
and
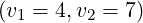 , with βth† = 0.001 and βth† = 0.1. In these simulations, pmax = 30, and uniform
momentum and pitch-angle grids are taken, with a size np = nξ0 ≃ 200 except when
specified.
, with βth† = 0.001 and βth† = 0.1. In these simulations, pmax = 30, and uniform
momentum and pitch-angle grids are taken, with a size np = nξ0 ≃ 200 except when
specified.
As shown in Fig.7.10, for all simulations with D0,newLH ranging from 1 to 10, the
conservative scheme is preserved, which clearly indicates the robustness of the discrete
projection of the Fokker-Planck equation on the numerical grid. Furthermore, from the
non-relativistic regime to the relativistic one, the ratio 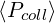 ∕
∕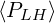 is close to 1, as expected
when the solution has a physical sense, i.e. when D0,newLH ≤ 2 only. It is interesting to observe
that the current drive efficiency does not vary significantly from D0,newLH = 1 to D0,newLH = 2,
which indicates that the saturated regime with a flat plateau is almost reached when
D0,newLH = 1.
is close to 1, as expected
when the solution has a physical sense, i.e. when D0,newLH ≤ 2 only. It is interesting to observe
that the current drive efficiency does not vary significantly from D0,newLH = 1 to D0,newLH = 2,
which indicates that the saturated regime with a flat plateau is almost reached when
D0,newLH = 1.
When D0,newLH exceeds 5, numerous numerical problems occur. For βth† = 0.001, the
value of the driven current has no sense, and may have also the wrong direction,
while the ratio 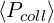 ∕
∕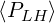 is always far from unity. This situation can never be
recovered by increasing the grid size up to np = nξ0 ≃ 300. The difference between
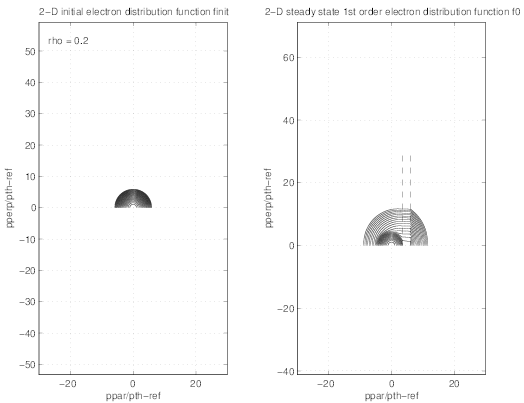
distribution functions given by the code with D0,newLH = 2 and D0,newLH = 10 is clearly
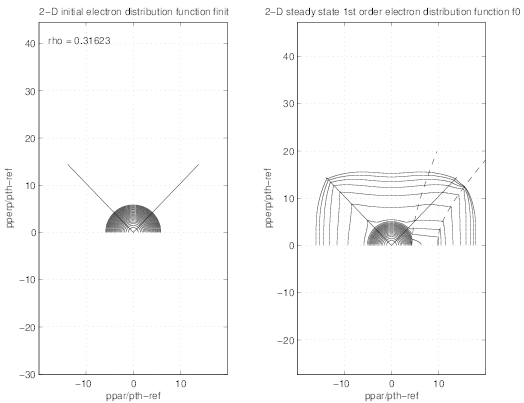
visible between contour plots in Figs.7.11 and 7.12, for the case
is always far from unity. This situation can never be
recovered by increasing the grid size up to np = nξ0 ≃ 300. The difference between
distribution functions given by the code with D0,newLH = 2 and D0,newLH = 10 is clearly
visible between contour plots in Figs.7.11 and 7.12, for the case 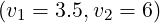 .
Spurious shapes appear for D0,newLH = 10 whose weight in the current drive efficiency
calculation is dramatic. Conversely, for D0,newLH = 2, the distribution function is well
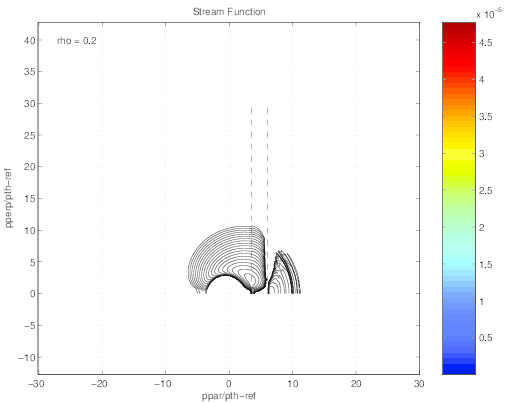
behaved, and the stream countours given in Fig.7.13 clearly have the expected physical
shape.
.
Spurious shapes appear for D0,newLH = 10 whose weight in the current drive efficiency
calculation is dramatic. Conversely, for D0,newLH = 2, the distribution function is well
behaved, and the stream countours given in Fig.7.13 clearly have the expected physical
shape.
Attempt to reduce this problem by smoothing the momentum variation of D0,newLH, in
particular the sharp transition at the resonance domain boundaries, turns out to be absolutely
useless. With a 5 points smoothing, the onset of numerical instabilities remains similar to the
one with sharp variations.
For the relativistic regime βth† = 0.1, the effect of increasing D0,newLH above 5 is more
subtile since in that case the current drive efficiency increases significantly, while 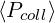 ∕
∕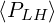 remains close to 1 within 20%. It is therefore very difficult to identify unambiguously that the
solution has no physical sense. In order to cross-check that the solution is wrong, the grid size
has been increased up to np = nξ0 ≃ 300. In that case, the effect is spectacular, and the current
drive efficient drops down to an acceptable level, while
remains close to 1 within 20%. It is therefore very difficult to identify unambiguously that the
solution has no physical sense. In order to cross-check that the solution is wrong, the grid size
has been increased up to np = nξ0 ≃ 300. In that case, the effect is spectacular, and the current
drive efficient drops down to an acceptable level, while 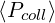 ∕
∕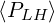 is very close to
unity for D0,newLH = 10 as shown, in Fig. 7.10. Still visible, this effect is weaker for
D0,newLH = 5.
is very close to
unity for D0,newLH = 10 as shown, in Fig. 7.10. Still visible, this effect is weaker for
D0,newLH = 5.
From this analysis, it is clear that a too coarse grid leads to strong limitations on the upper
value of D0,newLH that may be used for accurate estimate of the current drive level with
sharp variation of the Lower Hybrid quasilinear diffusion coefficient. It is clear that
this problem is enhanced in the non-relativistic regime, for an unknown reason yet.
Finally, a smooth transition from a solution that has a physical sense to a solution
that has no physical sense is clearly observed by increasing D0,newLH. There is no
evidence that this problem corresponds always to an increase of the current drive
efficiency. This difficulty is particularly difficult to handle, since no clear criterion
may help to reject the solution. Consequently, it is highly recommended to avoid
the use of the code with D0,newLH larger 2 to be free from numerical problems for
almost all situations. In any case, forcing the Maxwellian solution close to p = 0 and
normalizing the density at each iteration when numerical problems occur is usualy useless,
since the solution given by the code remain in general fully non physical, though
convergence can be ensured. In that case, the overall absorption process fails, and
the result has no meaning. A possible way to overcome this problem is to perform
calculations with the upper acceptable D0,newLH = 2 value, while using an adhoc
correcting factor, in order to recover the solution corresponding asymptotic limit at
D0,newLH = +∞.
From the physical point of view, it is not surprizing that the use of very large D0,newLH
values leads to numerical instabilities. Indeed, in that case, the characteristic quasilinear time in
the resonance domain is close to zero, with respect to the collision time. Consequently, there is
some degeneracy in the corresponding part of the matrix, since different regions of the
momentum space are instantaneoulsy connected at the collision scale. Therefore, parts of the
matrix do not provide additionnal information, but the numerical errors related to the
projection of the differential equations on the numerical grids act like a reservoir of numerical
instabilities in that case. There are some similarities with the implicit description of the trapped
electrons, when bounce-averaged Fokker-Planck equation must be solved. The only
and consistent way to solve this problem is to remove the domain where the time
ordering fails, and establish correct internal boundary conditions so that the density
of electron at v1 is exactly equal to the one at v2 at all pich-angles ξ0 grid points.
Obviously, this process adds new off-diagonal coefficients in the matrix, but in that case,
the conditionning of the matrix is preserved even for D0,newLH = +∞. With the
new general method of partial matrix factorization discussed in Sec.6.2.1, such an
approach may be in principle easily tractable, without prohibitive computational
efforts.
The role played by a non-uniform pitch-angle grid is critical, since in realistic simulations,
bounce-averaging must be considered with trapped-passing boundaries that moves in mometum
space with the radial position. In that region, the pitch-angle gris step must be lower,
for more accurate results. Concerning the momentum grid, as discussed in Sec.5.4.3
the domain where the grid is non-uniform, is by construction far from the region
where the quasilinear diffusion coefficient is different from zero, and consequently
all the results obtain for the uniform grid are valid. It is found that a non-uniform
pitch-angle grid has no effect for D0,newLH ≤ 2, np = nξ0 ≃ 200 and pmax = 30 on the
solution found by the code, within less than 1%, which is an important result for 3 - D
operation, even when Zs increases, and 2 - D broadening by pitch-angle scattering plays
progressively a dominant role over the parallel direction along the magnetic field line
direction.
Ultimate benchmarks have been performed to validate the implementation of the Lower
Hybrid current drive in the code in 3 - D configuration and relativistic regime, in presence of
bounce-averaging. The same radial grid introduced for the electrical conductivity
calculations in Sec. 7.1 is used, and flat profiles are considered, so that only the role
of trapped electrons comes into play. In Fig.7.14 , a typical case for D0,newLH = 1,
np = nξ0 ≃ 200 and pmax = 20 with 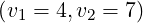 at ρ = 0.31623 is shown. This
corresponds to a similar inverse aspect ratio ϵ, since in this calculation ap ≃ Rp. Only a
part of the quasilinear domain at large p⊥ intercepts the trapped-passing boundary,
leading therefore to a modest reduction of the current drive efficiency, by 6% in this
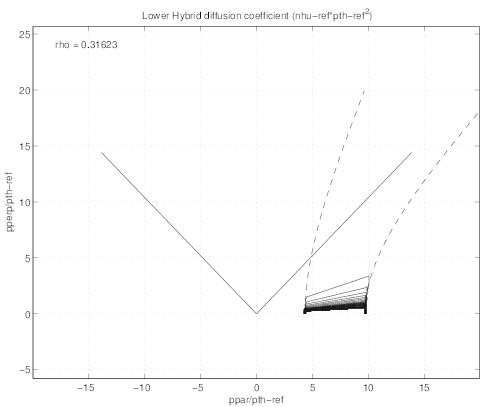
case. The contour plot of the corresponding quasilinear domain is shown in Fig. 7.15,
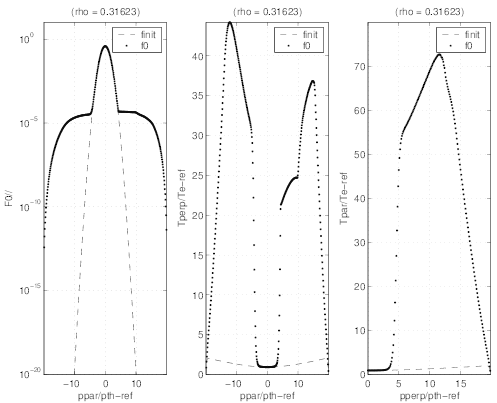
and in Fig.7.16 the 1 - D like distribution function F∥0
at ρ = 0.31623 is shown. This
corresponds to a similar inverse aspect ratio ϵ, since in this calculation ap ≃ Rp. Only a
part of the quasilinear domain at large p⊥ intercepts the trapped-passing boundary,
leading therefore to a modest reduction of the current drive efficiency, by 6% in this
case. The contour plot of the corresponding quasilinear domain is shown in Fig. 7.15,
and in Fig.7.16 the 1 - D like distribution function F∥0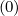
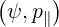 averaged over the
direction perpendicular to the magnetic field line direction, as well as the parallel
and perpendicular temperatures T∥ and T⊥. defined in Sec. No anomalous numerical
behaviour is observed. An important results is that the current drive efficiency does not
vary when the resonance domain is replaced by
averaged over the
direction perpendicular to the magnetic field line direction, as well as the parallel
and perpendicular temperatures T∥ and T⊥. defined in Sec. No anomalous numerical
behaviour is observed. An important results is that the current drive efficiency does not
vary when the resonance domain is replaced by 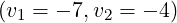 . Only the sign
of the current is reversed. Moreover, when a compound spectrum is launched, with
. Only the sign
of the current is reversed. Moreover, when a compound spectrum is launched, with
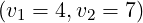 and
and 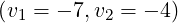 , the current level given by the code is zero
within the numerical accuracy, at least 3 orders of magnitude lower than for the case
, the current level given by the code is zero
within the numerical accuracy, at least 3 orders of magnitude lower than for the case
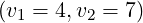 or
or 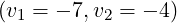 alone. This results confirm the robustness of the
numerical scheme, for complex and realistic modeling of the Lower Hybrid current drive
problem.
alone. This results confirm the robustness of the
numerical scheme, for complex and realistic modeling of the Lower Hybrid current drive
problem.
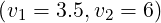 and
and 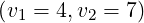 . Except it is specified, the default upper bound of
the integration domain is taken at pmax = 20. Plasma parameters are similar to those
used in Sec.7.1 dedicated to the the Ohmic conductivity problem, except that the
reference electron temperature may take two different values Te† = 5.11 × 10-4keV and
Te† = 5.11keV corresponding to non-relativistic to relativistic limits respectively. The choice of
these electron temperatures allows comparaison with already published results at
βth† = 0.01
. Except it is specified, the default upper bound of
the integration domain is taken at pmax = 20. Plasma parameters are similar to those
used in Sec.7.1 dedicated to the the Ohmic conductivity problem, except that the
reference electron temperature may take two different values Te† = 5.11 × 10-4keV and
Te† = 5.11keV corresponding to non-relativistic to relativistic limits respectively. The choice of
these electron temperatures allows comparaison with already published results at
βth† = 0.01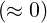 and βth† = 0.1. All corresponding plasma parameters are gathered
in section “CQL3D_LH” of the M-file “ptok_dke_1yp.m”, since it corresponds to
conditions that have been used for code comparison with the well known CQL3D code
[?].
and βth† = 0.1. All corresponding plasma parameters are gathered
in section “CQL3D_LH” of the M-file “ptok_dke_1yp.m”, since it corresponds to
conditions that have been used for code comparison with the well known CQL3D code
[?].
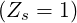
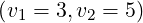
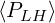 power density arises when
power density arises when 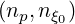
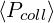 is not exactly equivalent to
is not exactly equivalent to 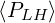
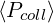
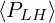
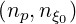
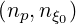
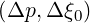
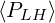 and
and 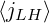 found by the code are larger by more than
10%. The difference arises likely from the collision operator that may exhibit some
differences.
found by the code are larger by more than
10%. The difference arises likely from the collision operator that may exhibit some
differences.
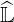 and
and 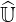 grows quadratically as expected from a 2
grows quadratically as expected from a 2 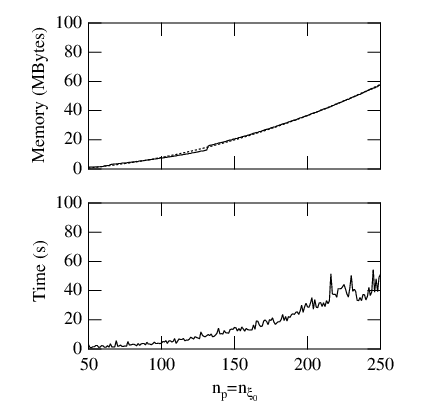
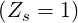
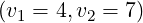 so that
so that 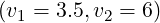
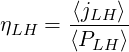
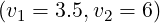 or
or 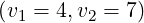
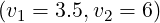 but also for
but also for 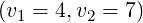 when the upper limit of the momentum
integration domain is
when the upper limit of the momentum
integration domain is 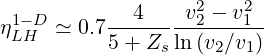
 with
with  . This factor could arise from that fact that the
1
. This factor could arise from that fact that the
1 ![[v1 = 3.5,v2 = 6]](NoticeDKE4256x.png)
![[v1 = 4,v2 = 7]](NoticeDKE4257x.png) which is close to the expected theoretical value 0
which is close to the expected theoretical value 0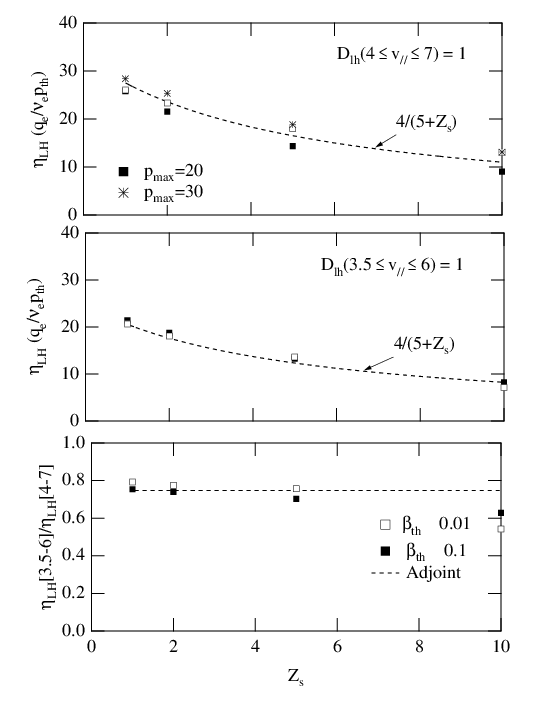
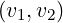
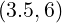
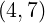
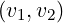
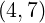
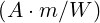 in a pure hydrogen plasma
from various 2
in a pure hydrogen plasma
from various 2 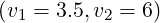 and
and
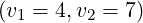
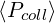
 is close to 1, as expected
when the solution has a physical sense, i.e. when
is close to 1, as expected
when the solution has a physical sense, i.e. when 
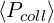
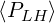 is always far from unity. This situation can never be
recovered by increasing the grid size up to
is always far from unity. This situation can never be
recovered by increasing the grid size up to 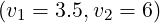 .
Spurious shapes appear for
.
Spurious shapes appear for 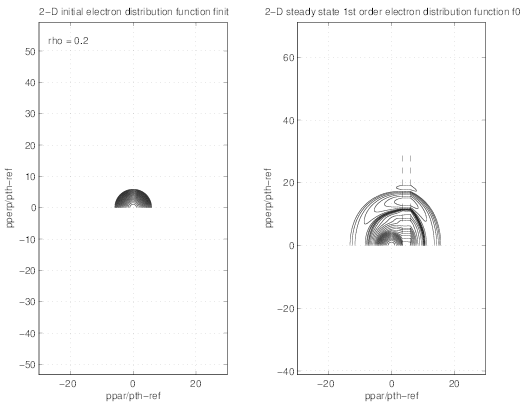
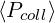
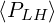 remains close to 1 within 20%. It is therefore very difficult to identify unambiguously that the
solution has no physical sense. In order to cross-check that the solution is wrong, the grid size
has been increased up to
remains close to 1 within 20%. It is therefore very difficult to identify unambiguously that the
solution has no physical sense. In order to cross-check that the solution is wrong, the grid size
has been increased up to 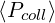
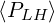 is very close to
unity for
is very close to
unity for 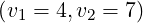 at
at 
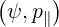 averaged over the
direction perpendicular to the magnetic field line direction, as well as the parallel
and perpendicular temperatures
averaged over the
direction perpendicular to the magnetic field line direction, as well as the parallel
and perpendicular temperatures 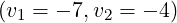
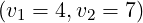 and
and 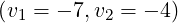
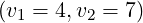 or
or 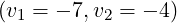 alone. This results confirm the robustness of the
numerical scheme, for complex and realistic modeling of the Lower Hybrid current drive
problem.
alone. This results confirm the robustness of the
numerical scheme, for complex and realistic modeling of the Lower Hybrid current drive
problem.