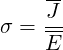
The determination of the Ohmic electrical conductivity
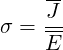 | (7.1) |
is a fundamental test for such kinetic codes. Extensive analysis have been performed to investigate code capabilities. To avoid the runaway problem, E = 0.01, and pmax = 15. Machine parameters are corresponding to non-relativistic limit Te† = 0.1keV, and a rather low density ne† = 10+19m-3 at the plasma center. Here, Ti† = ni† = 0. Except if it is specified, all profiles are flat. The dominant ion species is usually hydrogen, though some simulations have been done for deuterium. No impurities are considered, except for investigating the role of the effective charge. In order to investigate the effect of trapped particle, a simplified tokamak geometry is considered, with circular plasma cross-sections and neglecting any Shafranov shift. Except if it is mentionned, bounce integrals are performed analytically, according to the expressions given throughout the text. The minor radius is set to ap = 2.3899m and the major one is Rp = 2.39m so that the normalized radius ρ is very close to ϵ value from 0 to 1. In the tokamak parameter M-file “ptok_dke_1yp.m”, the corresponding section for these simulations is named “CQL3D_OHM”, since it corresponds to conditions that have been used for code comparison with the well know CQL3D program [?]. For all cases, except when notified, the drop tolerance level is set to 2 × 10-3. It has been also verified that the results are independent of this parameter, providing the convergence is achieved.
First local analysis have been performed, without considering bounce averaging. The role played by the collision operator is crucial on the driven current as shown in Table 7.1
| Collision operator | σ [DKE code] | σ [Karney] |
| Maxwellian | 3.7655 | 3.773 |
| High velocity | 3.0158 | 2.837 |
| Exact | 7.4406 | 7.429 |
An excellent agreement is found with Karney’s results [?], even with a coarse numerical grid
corresponding to np = 88 and nξ0 = 120. Some slight differences may arise from the different
form of the collision operators, and the number of grid points. In that case, the code is running
in a fully conservative mode, namely without normalization of the density at each
time step  , nor by forcing the Maxwellian solution at i = 1∕2 for the
momentum grid. When a more refined grid is used, slight evolutions are observed, and the
conductivity decreases from σ = 7.4406 down to σ = 7.4343, less than 0.1% for the exact
collision operator when np = 165, while nξ0 is kept constant. The role of the mass is
also fairly weak, since for the deuterium case, σ = 7.4471 for np = 88. Finally, by
increasing the integration domain up to pmax = 20, σ = 7.4387. The very small variation
confirms that no particle are leaving the domain of integration. which confirms that
7.4387.
, nor by forcing the Maxwellian solution at i = 1∕2 for the
momentum grid. When a more refined grid is used, slight evolutions are observed, and the
conductivity decreases from σ = 7.4406 down to σ = 7.4343, less than 0.1% for the exact
collision operator when np = 165, while nξ0 is kept constant. The role of the mass is
also fairly weak, since for the deuterium case, σ = 7.4471 for np = 88. Finally, by
increasing the integration domain up to pmax = 20, σ = 7.4387. The very small variation
confirms that no particle are leaving the domain of integration. which confirms that
7.4387.
As far as Zeff is increased, the Lorentz limit is progressively reached, since the pitch-angle predominates. This is clearly shown in Table 7.2
| Zeff | σ [DKE code] | σ [Karney] |
| 1 | 7.4353 | 7.429 |
| 2 | 4.3697 | 4.377 |
| 5 | 2.0619 | 2.078 |
| 10 | 1.1147 | 1.133 |
and in the limit Zeff ≫ 1, the result is well independent of the electron-electron collision model [?]. Its value is roughly given by expression
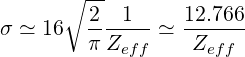 | (7.2) |
and the analytical limit is recovered by the code with Zeff ≃ 20.
A full 3 - D calculation has been performed with flat profiles at normalized radial
positions on the spatial flux grid ![[0.2,0.4,0.6,0.8]](NoticeDKE4210x.png) , giving the following radial positions
ρ =
, giving the following radial positions
ρ = ![[0.14142,0.31623, 0.5099,0.70711,0.90554]](NoticeDKE4211x.png) . In that case, the code calculates itself the
pitch-angle grid and the number of step is nξ0 = 168, while np = 125.The conductivity is found
to be independent of the method of calculations, and the value σ = 7.4353 is well recovered. It is
found that the code remains fully conservative without forcing the Maxwellian solution at
i = 1∕2 and without normalizing the density at each iteration.
. In that case, the code calculates itself the
pitch-angle grid and the number of step is nξ0 = 168, while np = 125.The conductivity is found
to be independent of the method of calculations, and the value σ = 7.4353 is well recovered. It is
found that the code remains fully conservative without forcing the Maxwellian solution at
i = 1∕2 and without normalizing the density at each iteration.
Bounce averaged calculations have be performed first locally. As shown in Fig. 7.1, an excellent agreement is found with CQL code from Ref. [?] over a broad range for the inverse aspect ratio, and also its more recent version CQL3D [?]. At the limit ϵ ≪ 1, the approximate Sigmar-Coppi expression
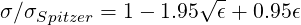 | (7.3) |
is well recovered. When ϵ ≃ 1, the value found by the code is very close to the asymptoytic limit given by the expression of Connor, as discussed in Ref. [?].
As shown in Fig. 7.1, in 3 - D mode, the agreement with theory and CQL(3D) codes remains fully very good, whatever the normalization reference of the electric field, at the plasma center, or at the local position. This result gives strong confidence to the code when kinetic calculations are simultaneously performed at various radial positions. Moreover, it has been cross-checked that the conductivity level is independent of the sign of the electric field, but also of the method used for calculating the bounce integrals. This latter point is crucial and demonstrates that numerical calculations of the bounce integrals is very accurate, even for finite inverse aspect ratio. The drop tolerance has been lowered in that case to 10-4 for ensuring a stable convergence, leading to a modest increase of the matrix sizes. However the rate of convergence is not affected, and the final result is obtained usually after 11 - 13 iterations, even when several radial positions are considered.