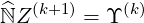
According to Sec. 6.1.1, the electron Fokker-Planck equation may be expressed in a general symbolic matrix form
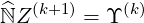 | (6.12) |
where Z = X with
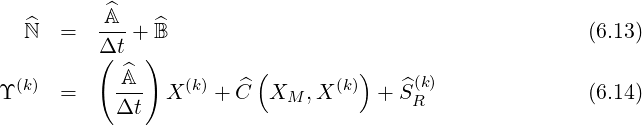
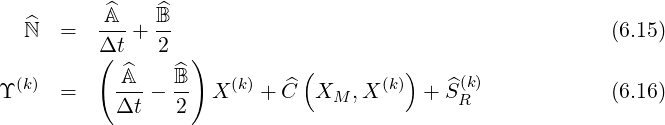
The formal expression (6.12) may be also used for the electron drift kinetic equation as shown in Sec. 6.1.2, and in this case, Z = Y with
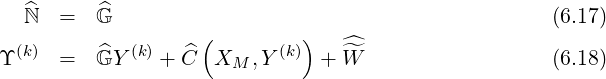
In all cases, matrices are square with similar structures, i.e. non-zero elements are aligned along a reduced number of diagonals which are roughly symmetricaly placed around the main one4, as shown in Fig.6.3. Consequently, the method for determining the asymptotic solution
cmcmcm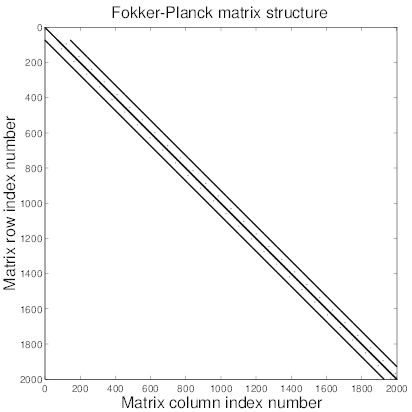
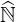 corresponding to the Fokker-Planck equation
corresponding to the Fokker-Planck equation
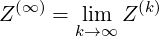 | (6.19) |
of the system of equations (6.12) will be the same, either for the Fokker-Planck or the drift kinetic equations.
In order to avoid manipulation of large matrix coefficients that may reduce the numerical accuracy and also leads often to numerical instabilities, main diagonal matrix preconditioning is first performed. The modified system of equation to solve is then
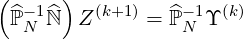 | (6.20) |
where all the coefficients of the main diagonal of matrix 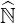 ′
′
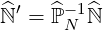 | (6.21) |
are one by definition. Here 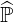 N is a diagonal matrix whose coefficients are those of the main
diagonal of
N is a diagonal matrix whose coefficients are those of the main
diagonal of 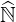 . Since collision is the dominant physics process, all off-diagonal coefficients are
usualy less than one, as shown in Fig.6.4, except when specific internal boundary conditions
apply, like at ξ0 = 0 in the trapped region.
. Since collision is the dominant physics process, all off-diagonal coefficients are
usualy less than one, as shown in Fig.6.4, except when specific internal boundary conditions
apply, like at ξ0 = 0 in the trapped region.
cmcmcm
 ′ corresponding to the Fokker-Planck equation. Dot points correspond to
pitch-angle process at constant p, while full line for slowing-down process at constant ξ0.
By definition values of all coefficients on the main diagonal are one
′ corresponding to the Fokker-Planck equation. Dot points correspond to
pitch-angle process at constant p, while full line for slowing-down process at constant ξ0.
By definition values of all coefficients on the main diagonal are one
The determination of Z(k+1) requires to invert the system of equation (6.12). The usual
method based on a direct inversion by the well known Gaussian elimination is immediately ruled
out, since the number of operations for each direction is 
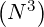 , where N is the number of rows
(or columns) of matrix
, where N is the number of rows
(or columns) of matrix 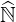 . For the example nψ = 20, np = 200 and nξ0 = 200 discussed in Sec.
6.1.1, N = nψnpnξ0 = 800000,
. For the example nψ = 20, np = 200 and nξ0 = 200 discussed in Sec.
6.1.1, N = nψnpnξ0 = 800000, 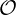
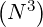 ≃ 10+17, corresponding to a prohibitive number of
operations. In addition, since memory requirements grow as
≃ 10+17, corresponding to a prohibitive number of
operations. In addition, since memory requirements grow as 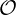
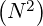 unacceptable storage
constraints take also place.
unacceptable storage
constraints take also place.
Consequently, alternative methods must be used, in order to perform a fast matrix inversion
without the need of a large memory storage requirement. The basic principle is to factorize 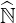 ′
into upper and lower triangular matrices
′
into upper and lower triangular matrices 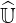 and
and 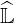 respectively
respectively
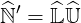 | (6.22) |
as shown in Fig. 6.5, that are themselves highly sparse matrices. A strong reduction of the
computational effort may then be foreseen, since the number of coefficients that are considered
in the calculations is considerably lower. Indeed, aside from the time required to perform the
matrix factorization itself which represents a computational effort equivalent to a direct matrix
inversion, each further inversion needs only 
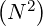 operations for each triangular system of
equations as shown in the next sections. Therefore, for large values of N, a substantial gain may
be expected, as soon as the number of iterations for an accurate estimate of the solution Z(∞) is
greater than unity. This is usually the case for the time dependent problem where all
time steps must be evaluated, but also when only the steady-state solution Z(∞) is
seeked, since the non-linearity resulting form self-collision operators
operations for each triangular system of
equations as shown in the next sections. Therefore, for large values of N, a substantial gain may
be expected, as soon as the number of iterations for an accurate estimate of the solution Z(∞) is
greater than unity. This is usually the case for the time dependent problem where all
time steps must be evaluated, but also when only the steady-state solution Z(∞) is
seeked, since the non-linearity resulting form self-collision operators 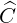 requires several
iterations either for the Fokker-Planck or the drift kinetic equations. This elegant
approach has been first considered for Fokker-Planck calculations for a five diagonals
operator as presented in Ref. [?], since in that case
requires several
iterations either for the Fokker-Planck or the drift kinetic equations. This elegant
approach has been first considered for Fokker-Planck calculations for a five diagonals
operator as presented in Ref. [?], since in that case 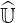 and
and 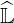 are both triangular and
tridiagonal matrices. However, as discussed in Ref. [?], the fact that cross-derivatives are
considered explicitely with respect to the time differencing scheme puts strong limitations.
Indeed, the integration time step Δt must be much lower than one for an accurate
determination of the solution of the set of linear equations. Consequently, the overall time
duration for calculating the steady-state solution is very long, an important drawback
when the kinetic solver must be incorporated in a chain of codes for realistic tokamak
simulations.
are both triangular and
tridiagonal matrices. However, as discussed in Ref. [?], the fact that cross-derivatives are
considered explicitely with respect to the time differencing scheme puts strong limitations.
Indeed, the integration time step Δt must be much lower than one for an accurate
determination of the solution of the set of linear equations. Consequently, the overall time
duration for calculating the steady-state solution is very long, an important drawback
when the kinetic solver must be incorporated in a chain of codes for realistic tokamak
simulations.
cmcmcm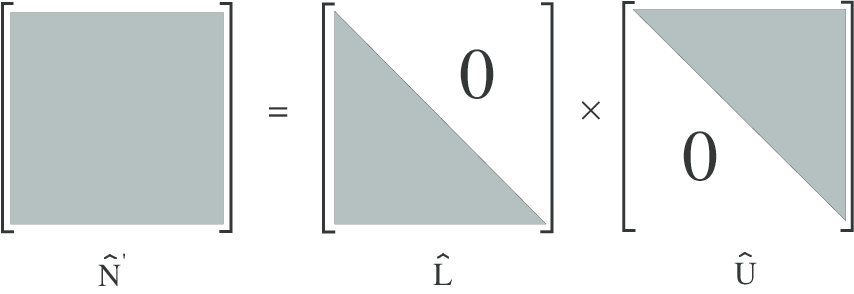
For this purpose, this method has been succesfully extended to the nine diagonals operator
case, allowing the use of much larger Δt values while the numerical scheme remains
stable, as shown in Ref. [?]. However, this approach is only useful for local kinetic
calculations, where trapped particle contribution is negligible, i.e. close to the plasma
center. When off-axis electron dynamics must be described, one must in that case fully
consider both circulating and trapped electron dynamics which leads to a number of
diagonals with non-zero elements that is much larger, fifteen diagonals at each radial
location as shown in Fig. 6.1. Therefore, the method developped for nine diagonal
operators may no more be used, since the number of operations to determine 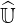 and
and 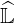 increases dramaticaly. The fully 3 - D approach with radial transport makes also this
method unusable, since the matrix that must be inverted has no more the nine diagonal
structure.
increases dramaticaly. The fully 3 - D approach with radial transport makes also this
method unusable, since the matrix that must be inverted has no more the nine diagonal
structure.
However, an equivalent form of the approximate matrix factorization may still be employed,
noting that exact 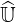 and
and 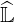 matrices are made of a large number of very small coefficients, close
to zero. This indicates that information on the electron dynamics is fully contained in a few set
of coefficients, whose number is several order of magnitude lower than the total one. Such a
structure results in fact from the well conditionning of the matrix
matrices are made of a large number of very small coefficients, close
to zero. This indicates that information on the electron dynamics is fully contained in a few set
of coefficients, whose number is several order of magnitude lower than the total one. Such a
structure results in fact from the well conditionning of the matrix 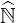 ′, a physical consequence
that collisions predominate over all other physical processes. Consequently, the general approach
is to introduce a non-negative scalar named as the drop tolerance parameter δlu, below
which small coefficients of exact
′, a physical consequence
that collisions predominate over all other physical processes. Consequently, the general approach
is to introduce a non-negative scalar named as the drop tolerance parameter δlu, below
which small coefficients of exact 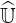 and
and 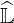 matrices are forced to zero. By this way, an
approximation of the exact matrix factorization is performed. The only exception to the
dropping rule is the diagonal of the upper triangular matrix which is preserved even if
coefficients are too small, in order to avoid singular factors. Since coefficients of
matrices are forced to zero. By this way, an
approximation of the exact matrix factorization is performed. The only exception to the
dropping rule is the diagonal of the upper triangular matrix which is preserved even if
coefficients are too small, in order to avoid singular factors. Since coefficients of 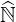 ′ lie
between 0 and 1 in the limit where the model holds, because of the main diagonal
preconditioning, the drop tolerance parameter δlu may be arbitrarily chosen in the same interval,
i.e.
′ lie
between 0 and 1 in the limit where the model holds, because of the main diagonal
preconditioning, the drop tolerance parameter δlu may be arbitrarily chosen in the same interval,
i.e.
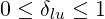 | (6.23) |
and when δlu is close to 0, approximate and exact matrices  and
and  are roughly equivalent,
while they differ strongly when δlu tends to one. In the latter case, considerable saving may be
foreseen for the memory requirement, as well as a significant reduction of the computer time
consumption, since less non-zero coefficients must be considered. An example is shown in Fig.
6.6, where δlu varies from zero to 10-2. Consequently, from the exact matrix factorization
to the approximate one, the number of non-zero elements drops by a factor around
30.
are roughly equivalent,
while they differ strongly when δlu tends to one. In the latter case, considerable saving may be
foreseen for the memory requirement, as well as a significant reduction of the computer time
consumption, since less non-zero coefficients must be considered. An example is shown in Fig.
6.6, where δlu varies from zero to 10-2. Consequently, from the exact matrix factorization
to the approximate one, the number of non-zero elements drops by a factor around
30.
cmcmcm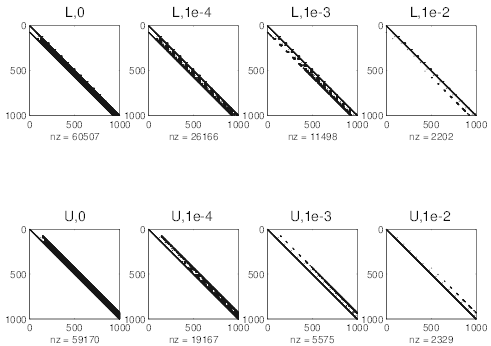
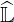 and
and  matrices, by increasing
δlu. Values of δlu are indicated on the top of each subfigure. For δlu = 10-2, the inversion
becomes instable.
matrices, by increasing
δlu. Values of δlu are indicated on the top of each subfigure. For δlu = 10-2, the inversion
becomes instable.
The rule is therefore to find the largest δlu value that is compatible with a stable inversion
procedure, even in presence of a large Ohmic electric field or a high RF power. However too
large δlu values will remove important physical informations, leading to spurious solutions.
However, it turns out that margins are usually considerable, making the method very effective.
An example is given in Fig. 6.7, which illustrates the effectiveness of the method,
for the Lower Hybrid current drive local problem. For δlu ≃ 2 × 10-3, memory size
requirement to store matrices 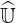 and
and 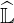 does not exceed 2.2MBytes, while it reaches
66MBytes when δlu = 0. It is interesting to observe that the convergence rate towards the
steady-state solution Z(∞) is reduced by 50%, and that the result is moreover independent
of δlu. For larger δlu values, the inversion scheme becomes progressively unstable,
and the benefit gains on the memory storage requirement is therefore cancelled by a
reduced rate of convergence. For this reason, the upper value used in the code is usually
δlu ≃ 2 × 10-3. More refined methods may be used to optimized the choice of δlu. The
trade-off that must be found between memory saving and stability of the inversion
procedure requires extensive investigations that are beyond the scope of this document.
Hopefully, it turns out that the domain 1 × 10-4 ≤ δlu ≤ 2 × 10-3 covers must of
the parameter range for the current drive problem in tokamaks, even in presence
of radial transport. Since the local problems needs only 2.2MBytes, it is therefore
possible to extrapolate that the full 3 - D problem with 20 radial positions will only
require approximately 44MBytes. This result has justified the development of this new
approach.
does not exceed 2.2MBytes, while it reaches
66MBytes when δlu = 0. It is interesting to observe that the convergence rate towards the
steady-state solution Z(∞) is reduced by 50%, and that the result is moreover independent
of δlu. For larger δlu values, the inversion scheme becomes progressively unstable,
and the benefit gains on the memory storage requirement is therefore cancelled by a
reduced rate of convergence. For this reason, the upper value used in the code is usually
δlu ≃ 2 × 10-3. More refined methods may be used to optimized the choice of δlu. The
trade-off that must be found between memory saving and stability of the inversion
procedure requires extensive investigations that are beyond the scope of this document.
Hopefully, it turns out that the domain 1 × 10-4 ≤ δlu ≤ 2 × 10-3 covers must of
the parameter range for the current drive problem in tokamaks, even in presence
of radial transport. Since the local problems needs only 2.2MBytes, it is therefore
possible to extrapolate that the full 3 - D problem with 20 radial positions will only
require approximately 44MBytes. This result has justified the development of this new
approach.
cmcmcm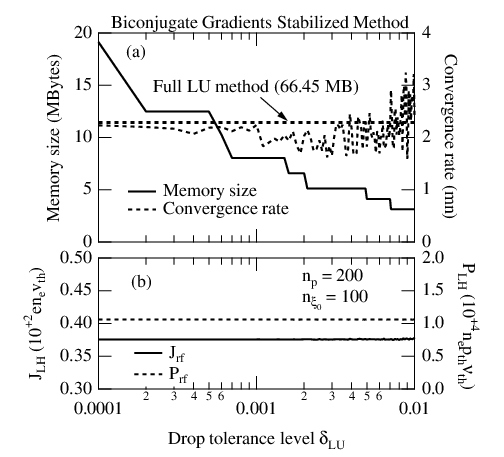
The matrix inversion procedure is based on the possibility of matrix factorization as discussed in Sec.6.2.1. Formally, the iterative method may be expressed in the simple form
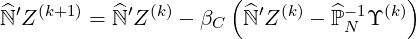 | (6.24) |
where βC is the iteration parameter that may be adjusted for an improvement of the rate of
convergence, using a Chebyshev acceleration technique as shown in Ref. [?]. Here 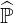 is
used for the main diagonal precondiotiong as explained in Sec.6.2.1 . However, it has
been shown that values of βC other than unity do not give much better results in
general for implicit methods ([?]), and therefore, only the case βC = 1 is considered.
Then Eq. 6.24 is equivalent to Eq. 6.12 given in Sec. 6.2.1. Replacing
is
used for the main diagonal precondiotiong as explained in Sec.6.2.1 . However, it has
been shown that values of βC other than unity do not give much better results in
general for implicit methods ([?]), and therefore, only the case βC = 1 is considered.
Then Eq. 6.24 is equivalent to Eq. 6.12 given in Sec. 6.2.1. Replacing 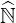 ′ by
′ by 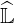
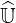 , one
obtains
, one
obtains
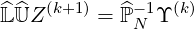 | (6.25) |
If we introduce the increment ΔZ(k+1)
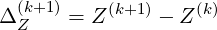 | (6.26) |
and the residual RZ(k)
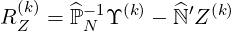 | (6.27) |
Eq.6.25 becomes simply
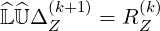 | (6.28) |
which can be solved by two successive inversion steps, evaluating respectively forward and backward solutions from triangular systems of equations

For achieving convergence towards the steady state solution Z(∞), various iterative methods may be used, like the Conjugate Gradient Squared (CGS), the BiConjigate Gradient (BICG) or the Quasi-Minimal Residual (QMR) methods. These methods, which both give equivalent results in term of convergence rate, are preferred to the BiConjigate Gradient Stabilized (BICGSTAB) method, since the conservative scheme is nearly always well fullfiled even for marginaly well-conditionned matrices, like in presence of RF waves whose intensity is large. All methods here considered are build-in MatLab functions whose principle may be found in Refs. [?] or [?] for more detailed insights.
After numerous tests, it has been found that the drop tolerance parameter δlu has a close link with the maximum number of iterations MAXIT allowed inside the function that performs the iterative matrix inversion, in order to avoid cumulative numerical errors that lead usually to violation of the conservative nature of the code. Even if this problem may be cured by forcing the Maxwellian solution close to p = 0 and normalizing the solution at each iteration, this approach has not been considered, because it may hinder more serious problems regarding the overall numerical conservative scheme. So far, a very robust and fully conservative scheme is achieved with the following rule of thumb
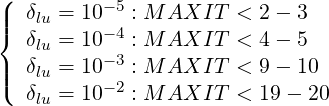 | (6.31) |
for all cases addressed by the code, including the in presence of RF waves. More detailed studied are necessary to clarify this point.
At each iteration, Z(k+1) is evaluated from the knowledge of ΔZ(k+1), and the electron
distribution function f0,l+1∕2,i+1∕2,j+1∕2 is reconstructed in order to evaluate the non-linear
term
is reconstructed in order to evaluate the non-linear
term 
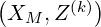 that arises from self-collisions. Though this procedure is quite time
consuming, its incidence on the overall time for converging is fairly marginal, since the number
of iterations never exceeds 10 in most cases.
that arises from self-collisions. Though this procedure is quite time
consuming, its incidence on the overall time for converging is fairly marginal, since the number
of iterations never exceeds 10 in most cases.
According to Ref. [?], convergence towards Z(∞) is considered to be achieved and the iteration is stopped when the following criterion is fullfiled
![┌│ ---∫∫ [-------]2---------------
││ 2π ∂f (00)∕∂t f0(0)JpJξ0dpdξ0
∘ --------∫∫--------------------< RfC
2π f(00)JpJξ0dpdξ0](NoticeDKE4052x.png) | (6.32) |
for an arbitrarily small 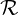
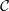 f, at all plasma locations ψ, where Jp and Jξ0 are the partial Jacobians as introduced
in Sec. 3.5.15.
f, at all plasma locations ψ, where Jp and Jξ0 are the partial Jacobians as introduced
in Sec. 3.5.15.
Projected on the numerical grid, the criterion (6.32) becomes
![⌊
i=n∑p-1 j=n∑ξ0-1[ (0)(k+1) (0)(k) ]2
⌈ f0,l+1∕2,i+1∕2,j+1∕2 - f0,l+1∕2,i+1∕2,j+1 ∕2
i=0 j=0](NoticeDKE4053x.png) | |||
![(0)(k) 2 ]
×f 0,l+1∕2,i+1 ∕2,j+1∕2pi+1∕2Δpi+1∕2Δξ0,j+1∕2](NoticeDKE4054x.png) 1∕2 1∕2 | |||
×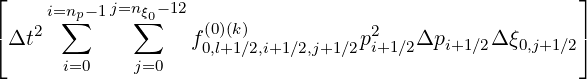 -1∕2 -1∕2 | |||
< 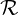 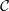 f f | (6.33) |
The criterion introduced in Ref. [?] has the main advantage to ensure that convergence is
achieved not for electrons whose energy is close to the thermal one, but also for the fastest when
a tail is driven by an external source. Usually, 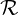
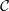 f ranges between 10-10 and 10-12, and in the
code the standard value is 10-11. The quantity (6.32) may be viewed as a norm, and its
definition is consequently independent of the level of current which results from the the
lack of symmetry of f0
f ranges between 10-10 and 10-12, and in the
code the standard value is 10-11. The quantity (6.32) may be viewed as a norm, and its
definition is consequently independent of the level of current which results from the the
lack of symmetry of f0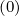 in momentum space. It may therefore be used for strong
deformations of the electron distribution function, even if the net current is close to
zero.
in momentum space. It may therefore be used for strong
deformations of the electron distribution function, even if the net current is close to
zero.
In practice, the total number of iteration 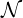
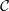 f is a free choice. It is usually set to 50, so that
inversion procedure stops when (6.32) is fullfiled in quite all cases. If the number of iterations
reaches
f is a free choice. It is usually set to 50, so that
inversion procedure stops when (6.32) is fullfiled in quite all cases. If the number of iterations
reaches 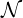
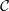 f, the program warns that convergence is not achieved and that something is going
wrong in the calculations. This may occur sometimes when too large quasilinear RF diffusion
coefficient are used, leading to inconsistent and non physical solutions. This point is extensively
discussed in Sec.7.3. Conversely, when time step is very large, i.e. Δt ≥ 1000, the convergence
may be achieved for a given value
f, the program warns that convergence is not achieved and that something is going
wrong in the calculations. This may occur sometimes when too large quasilinear RF diffusion
coefficient are used, leading to inconsistent and non physical solutions. This point is extensively
discussed in Sec.7.3. Conversely, when time step is very large, i.e. Δt ≥ 1000, the convergence
may be achieved for a given value 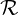
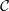 f before the current level is fully established.
Such an event may arise because there is a too reduced number of iterations which
involves the 1st order Legendre non-linear correction term for momentum conservation.
Consequently, to avoid this problem, a minimum number of iterations has been set to 6,
which turns out to be enough for giving reliable results, owing to the weakness of the
non-linearity.
f before the current level is fully established.
Such an event may arise because there is a too reduced number of iterations which
involves the 1st order Legendre non-linear correction term for momentum conservation.
Consequently, to avoid this problem, a minimum number of iterations has been set to 6,
which turns out to be enough for giving reliable results, owing to the weakness of the
non-linearity.
The inversion procedure for solving the first order drift kinetic equation is exactly similar to the
one described in Sec. 6.2.2. Indeed, the linear system of equation to be solved may be cast in a
similar form. Usually, the convergence coefficient 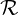
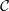 g is set to similar values than for the
Fokker-Planck problem, while the maximum number of iterations allowed
g is set to similar values than for the
Fokker-Planck problem, while the maximum number of iterations allowed 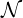
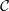 g is slightly larger
6, since
the convergence requires more iterations, around 20 - 30. Since the function g0
g is slightly larger
6, since
the convergence requires more iterations, around 20 - 30. Since the function g0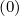 may be
negative and that dt has no sense here, as the solution is determined once the steady-state
regime is achieved, the convergence criterion is modified accordingly
may be
negative and that dt has no sense here, as the solution is determined once the steady-state
regime is achieved, the convergence criterion is modified accordingly
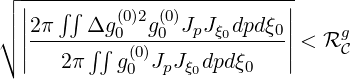 | (6.34) |
at all plasma locations ψ. Here again Jp and Jξ0 are the partial Jacobians introduced in Sec. 3.5.17.
Projected on the numerical grid, the criterion (6.34) becomes
![|
||i=∑np-1j=n∑ξ0-1[ (0)(k+1) (0)(k) ]2
|| g0,l+1∕2,i+1 ∕2,j+1∕2 - g0,l+1∕2,i+1∕2,j+1∕2
| i=0 j=0](NoticeDKE4059x.png) | |||
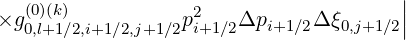 1∕2 1∕2 | |||
×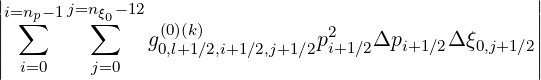 -1∕2 < -1∕2 < 
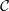 g g | (6.35) |
where 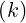 is the iteration step number. Since all quantities are normalized, this definition is
fully acceptable. If the number of iterations reaches
is the iteration step number. Since all quantities are normalized, this definition is
fully acceptable. If the number of iterations reaches 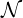
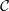 g, the program warns that convergence is
not achieved and that something is going wrong in the calculations, as for the Fokker-Planck
part.
g, the program warns that convergence is
not achieved and that something is going wrong in the calculations, as for the Fokker-Planck
part.