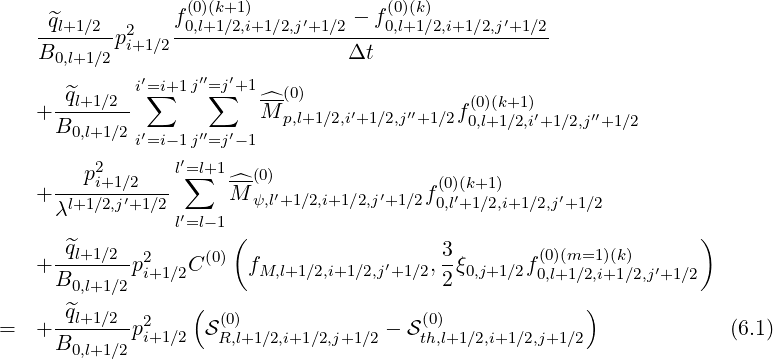
Projected on the numerical distribution function grid, and taking into account of the internal and external boundaries, the 3 - D electron Fokker-Planck equation may be expressed as
where C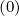 is the first order Legendre electron-electron self-collision term that ensures
momentum conservation, as discussed in Sec.4.1.1 , a contribution that introduces a weak
non-linear dependence,
is the first order Legendre electron-electron self-collision term that ensures
momentum conservation, as discussed in Sec.4.1.1 , a contribution that introduces a weak
non-linear dependence, 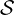 R,l+1∕2,i+1∕2,j+1∕2
R,l+1∕2,i+1∕2,j+1∕2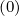 is the runaway avalanche source term as introduced
in Sec.3.6 and
is the runaway avalanche source term as introduced
in Sec.3.6 and 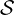 th,l+1∕2,i+1∕2,j+1∕2
th,l+1∕2,i+1∕2,j+1∕2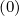 is the source of thermal that must be removed from the
bulk since they have been knock-on to much higher energies. Here, the Fokker-Planck equation
(6.1) is evaluated on the reduced pitch-angle grid which is described by the index number
j′.
is the source of thermal that must be removed from the
bulk since they have been knock-on to much higher energies. Here, the Fokker-Planck equation
(6.1) is evaluated on the reduced pitch-angle grid which is described by the index number
j′.
Upwind differencing corresponding to the fully implicit time scheme is used, since it is usually
numerically stable for arbitrary values of Δt. Therefore, with this method, a fast rate of convergence
towards the steady-state solution limk→∞f0,l+1∕2,i+1∕2,j′+1∕2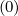 (k+1) = f0,l+1∕2,i+1∕2,j′+1∕2
(k+1) = f0,l+1∕2,i+1∕2,j′+1∕2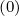 (∞) may
be achieved, using extremely large time step Δt, with respect to the usual collision reference time
τc† as discussed in Sec. 6.3. The fact that both momentum and spatial dynamics are considered
simultaneously represents a considerable progress as compared to the standard operator splitting
technique1,
where alternatively, dynamics in each space are considered explicitely, a procedure which puts
strong limitations on the time step Δt∕τc†≈ 1.
(∞) may
be achieved, using extremely large time step Δt, with respect to the usual collision reference time
τc† as discussed in Sec. 6.3. The fact that both momentum and spatial dynamics are considered
simultaneously represents a considerable progress as compared to the standard operator splitting
technique1,
where alternatively, dynamics in each space are considered explicitely, a procedure which puts
strong limitations on the time step Δt∕τc†≈ 1.
In compact matrix form, the differential equation in the reduced momentum phase space has the following symbolic form
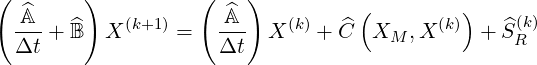 | (6.2) |
where 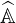 is a single diagonal matrix associated to time differencing,
is a single diagonal matrix associated to time differencing, 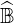 corresponds to the flux
divergence and
corresponds to the flux
divergence and 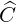 is the first order Legendre correction, and
is the first order Legendre correction, and 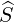 R is the runaway avalanche source
term. Here X(k) is a vector whose components are the discrete values of the distribution function
f0
R is the runaway avalanche source
term. Here X(k) is a vector whose components are the discrete values of the distribution function
f0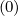 at time step
at time step 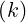 , organized as follows
, organized as follows
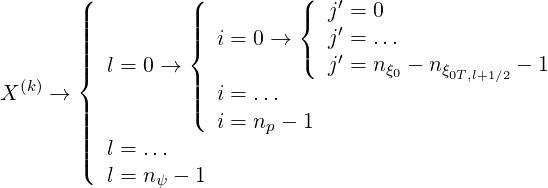 | (6.3) |
while XM corresponds to the Maxwellian distribution function.
Without radial transport, 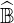 is a block diagonal matrix. Each block, which describes the
momentum dynamics at location ψl+1∕2, is a square matrice of 15 diagonals whose size
is a block diagonal matrix. Each block, which describes the
momentum dynamics at location ψl+1∕2, is a square matrice of 15 diagonals whose size
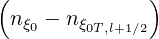 np×
np×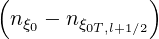 np progressively decreases from ψ1∕2 to ψnξ
0-1∕2
because of the trapped/passing boundary enlarges from the center to the plasma edge, as shown
in Fig. 6.1. The main diagonal of
np progressively decreases from ψ1∕2 to ψnξ
0-1∕2
because of the trapped/passing boundary enlarges from the center to the plasma edge, as shown
in Fig. 6.1. The main diagonal of  is dominant because collisions predominate over other
physical processes at each plasma radius.
is dominant because collisions predominate over other
physical processes at each plasma radius.
The introduction of the radial dynamics adds several extra off-diagonals, which connect
neighboring blocks corresponding to different radial positions, in addition to the main diagonal
which is also modified accordingly. The complexity arises from the fact that trapped electrons
may become passing as a result of the radial transport process, and conversely. However, matrix
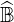 keeps a global banded structure and is still highly sparce, a property that is extensively
used for reducing memory storage requirement. Indeed, size of
keeps a global banded structure and is still highly sparce, a property that is extensively
used for reducing memory storage requirement. Indeed, size of 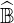 is roughly given by
relation
is roughly given by
relation
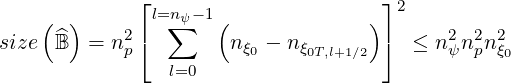 | (6.4) |
For tokamak with very large aspect ratio, size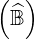 ≈ nψ2np2nξ02 since trapped
particle contribution is fairly negligible. In this limit, an upper boundary of the memory
size requirement may be estimated. For the reference case, nψ = 20, np = 200 and
nξ0 = 200, the total number of coefficients reaches 64 × 10+10, and the needed memory
capacity2
is 5.12TBytes ! Hopefully, this huge number may be drastically reduced
down to 11 × nψnpnξ0, since
≈ nψ2np2nξ02 since trapped
particle contribution is fairly negligible. In this limit, an upper boundary of the memory
size requirement may be estimated. For the reference case, nψ = 20, np = 200 and
nξ0 = 200, the total number of coefficients reaches 64 × 10+10, and the needed memory
capacity2
is 5.12TBytes ! Hopefully, this huge number may be drastically reduced
down to 11 × nψnpnξ0, since 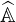 becomes in that limit a simple banded matrix
with exactly 11 diagonals. The required memory falls down therefore to
70.4MBytes3,
a level which can be easily handled by most computers today.
becomes in that limit a simple banded matrix
with exactly 11 diagonals. The required memory falls down therefore to
70.4MBytes3,
a level which can be easily handled by most computers today.
The Crank-Nicholson time scheme is used for time evolution studies of the distribution function
f0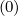 . It is second order accurate in time, but this scheme requires usualy Δt∕τc†≈ 1, in order
to avoid spurious numerical oscillations towards the steady-state solution f0
. It is second order accurate in time, but this scheme requires usualy Δt∕τc†≈ 1, in order
to avoid spurious numerical oscillations towards the steady-state solution f0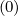
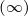 .
From Eq.6.2, it is straightforward to derive the new matrix form of the Fokker-Planck
equation
.
From Eq.6.2, it is straightforward to derive the new matrix form of the Fokker-Planck
equation
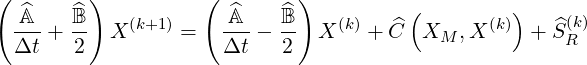 | (6.5) |
by just replacing
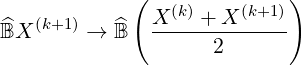 | (6.6) |
since 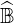 is a linear operator.
is a linear operator.
Projected on the numerical distribution function grid, and taking into account of the internal and external boundaries, the 3 - D electron drift kinetic equation may be expressed as
where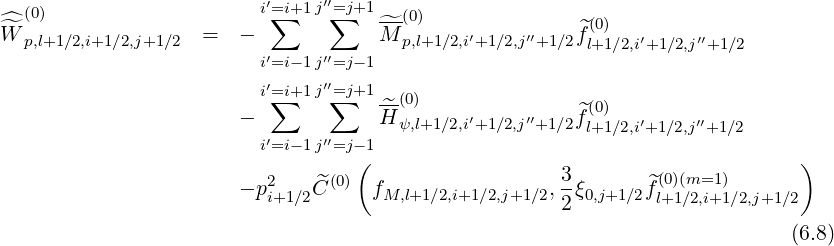
As mentioned in Sec.5.7.2, j →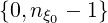 , while j′ →
, while j′ →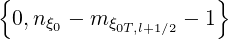 corresponds to the reduced pitch-angle grid which depends of the radial position ψl+1∕2, since all
the trapped region has been removed. In Eq.6.7, time evolution is not considered, since function
g
corresponds to the reduced pitch-angle grid which depends of the radial position ψl+1∕2, since all
the trapped region has been removed. In Eq.6.7, time evolution is not considered, since function
g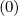 is only determined for steady-state value of
is only determined for steady-state value of 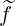
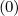 . Therefore, iterations to reach the solution
only result from the non-linear electron self-collision operator C
. Therefore, iterations to reach the solution
only result from the non-linear electron self-collision operator C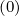 , that ensures momentum
conservation, in order to find a self-consistent solution.
, that ensures momentum
conservation, in order to find a self-consistent solution.
In compact matrix form, the differential equation in the reduced momentum phase space has the following symbolic form
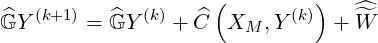 | (6.9) |
where 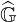 corresponds to the flux divergence,
corresponds to the flux divergence, 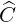 is the first order Legendre correction and
is the first order Legendre correction and  to
the contribution of the radial gradient of the distribution function f0
to
the contribution of the radial gradient of the distribution function f0 . Here Y (k) is a vector
whose components are the discrete values of the distribution function g
. Here Y (k) is a vector
whose components are the discrete values of the distribution function g
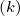 at iteration step
at iteration step
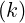 , organized as follows
, organized as follows
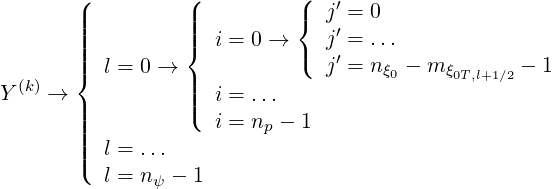 | (6.10) |
and vector XM is corresponding to the Maxwellian distribution function, as defined in Sec. 6.1.1.
By construction, 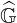 is simply a block diagonal matrix. Each block, which describes the
momentum dynamics at location ψl+1∕2, is a square matrice of 9 diagonals whose size
is simply a block diagonal matrix. Each block, which describes the
momentum dynamics at location ψl+1∕2, is a square matrice of 9 diagonals whose size
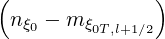 np×
np×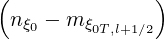 np progressively decreases from ψ1∕2 to ψnξ
0-1∕2
because of the trapped/passing boundary enlarges from the center to the plasma edge, as shown
in Fig. 6.2. The main diagonal of
np progressively decreases from ψ1∕2 to ψnξ
0-1∕2
because of the trapped/passing boundary enlarges from the center to the plasma edge, as shown
in Fig. 6.2. The main diagonal of 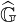 is also dominant because collisions predominate over other
physical processes at each plasma radius.
is also dominant because collisions predominate over other
physical processes at each plasma radius.
The matrix 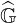 has a global banded structure with an extremely high sparcity, a property that
is also extensively used for memory storage, like for the Fokker-Planck equation (see Sec. 6.1.1).
Indeed, the size of
has a global banded structure with an extremely high sparcity, a property that
is also extensively used for memory storage, like for the Fokker-Planck equation (see Sec. 6.1.1).
Indeed, the size of 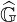 is roughlu given by relation
is roughlu given by relation
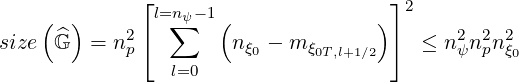 | (6.11) |
For tokamak with very large aspect ratio, size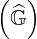 ≈ nψ2np2nξ02 since trapped particle
contribution is fairly negligible. In this limit, size
≈ nψ2np2nξ02 since trapped particle
contribution is fairly negligible. In this limit, size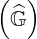 ≃ size
≃ size , where
, where 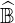 is the
flux matrix of the Fokker-Planck equation. For the values of nψ, np and nξ0 taken in
Sec. 6.1.1, the required memory is approximately 57.6MBytes, a lower level than for
the Fokker-Planck equation, since the trapped region is completely removed in the
calculations.
is the
flux matrix of the Fokker-Planck equation. For the values of nψ, np and nξ0 taken in
Sec. 6.1.1, the required memory is approximately 57.6MBytes, a lower level than for
the Fokker-Planck equation, since the trapped region is completely removed in the
calculations.