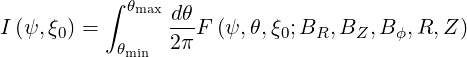
The numerical calculation of bounce coefficients requires an integration over θ which can be expressed symbolically as
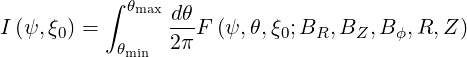 | (5.1) |
where BR,BZ,Bϕ,R,Z are functions of  . They are given on a uniform grid of Nθ points in
θ
. They are given on a uniform grid of Nθ points in
θ
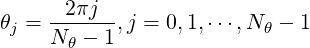 | (5.2) |
Domain of Integration
It is very important to account for the entire bounce path of the particle, including in
particular the tip of banana orbits near θT min and θT max. The contribution of these banana tips
is often larger than the dθ = 2π∕(Nθ - 1) accuracy level, because F can become very
large near the turning points. This is true for example in the calculation of λ, since
F
can become very
large near the turning points. This is true for example in the calculation of λ, since
F ~ 1∕ξ and ξ → 0 at the turning points. It is therefore crucial to perform the
integration up to θT min and θT max. However, these boundaries are defined by (2.28) and
(2.29)
~ 1∕ξ and ξ → 0 at the turning points. It is therefore crucial to perform the
integration up to θT min and θT max. However, these boundaries are defined by (2.28) and
(2.29)
 | (5.3) |
which in general do not coincide with a grid points. In order to calculate θT , we impose that the
values of the data BR,BZ,Bϕ,R,Z in θT be obtained by linear interpolation, while the value of
B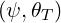 is obtained from (2.30).
is obtained from (2.30).
We consider the magnetic field Bb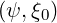 at the turning point θT min to be located between
the two (consecutive) values B1
at the turning point θT min to be located between
the two (consecutive) values B1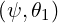 and B2
and B2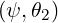 on the
on the  grid. These values
are determined from the three components issued by the equilibrium code simply by
grid. These values
are determined from the three components issued by the equilibrium code simply by
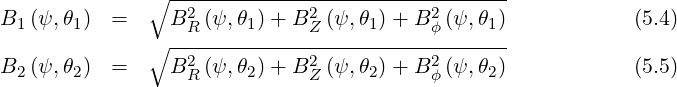
We choose to define the values of BR, BZ and Bϕ at the location θT by linear interpolation:
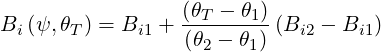 | (5.6) |
where i = R,Z,ϕ. Then, the location θT of the turning point can be calculated by requiring that the relation
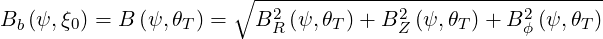 | (5.7) |
be satisfied. This implies
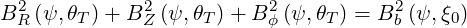 | (5.8) |
and then
![∑ [ (θT - θ1) ]2
Bi1 + ---------(Bi2 - Bi1) - B2b (ψ, ξ0) = 0
i=R,Z,ϕ (θ2 - θ1)](NoticeDKE2670x.png) | (5.9) |
Defining
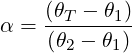 | (5.10) |
we find
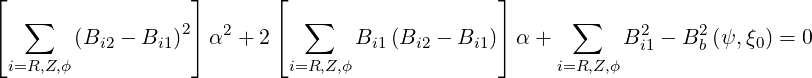 | (5.11) |
which solves as
![∘ -∑--------------------[∑-------------][∑----------]- ∑
± [ iBi1(Bi2 - Bi1)]2 - i(Bi2 - Bi1)2 iB2i1 - B2b - iBi1(Bi2 - Bi1)
α = ------------------------------∑--------------------------------------------
i(Bi2 - Bi1)2](NoticeDKE2673x.png) | (5.12) |
We have
![┌ -------------------------------------------------------------
│ [ ]2 [ ][ ]
│∘ ∑ B (B - B ) - ∑ (B - B )2 ∑ B2 - B2 (ψ, ξ)
i1 i2 i1 i2 i1 i1 b 0
∘ ---i---------------------i-----------------i-----------
(BR1BR2 + BZ1BZ2 + Bϕ1B ϕ2)2 - B21B22
= + [B2 + B2 - 2(BR2BR1 + BZ2BZ1 + B ϕ2Bϕ1)]B2 (ψ,ξ0)
∘ -----2-----1-------------------- b
= (Y - B2 )2 - (B2 - B2 )(B2 - B2 ) (5.13)
b b 1 b 2](NoticeDKE2674x.png)
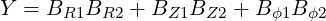 | (5.14) |
so that
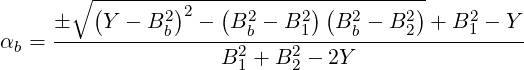 | (5.15) |
and finally
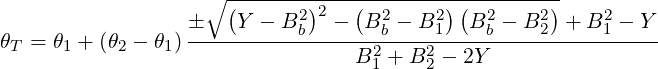 | (5.16) |
We must choose (numerically) the solution that gives 0 ≤ αb ≤ 1. Note that if the magnetic fields in points 1 and 2 are equal, we have Y = B12 = B22 = Bb2.
Numerical Integration
Once the two turning points have been added to the θ grid, now noted 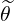 j, j = 0,1,2,
j, j = 0,1,2, Nθ + 1,
we define the half grid
Nθ + 1,
we define the half grid
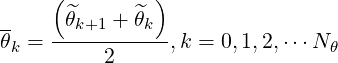 | (5.17) |
and calculate the discrete function
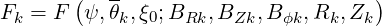 | (5.18) |
where BRk,BZk,Bϕk,Rk,Zk have been calculated on the grid θk by linear interpolation, and the step dθk, defined by
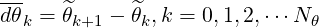 | (5.19) |
so that the integral becomes
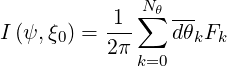 | (5.20) |