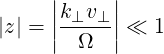 | (D.1) |
This condition generally holds for LHW and ECW as long as the temperature is not too high (T ≤ 10 keV) and the resonance harmonic is low (n = 0,1,2).
In this section, we use the cold plasma model to calculate the wave properties. This approximation is valid only if the following conditions are satisfied:
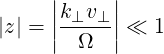 | (D.1) |
This condition generally holds for LHW and ECW as long as the temperature is not too high (T ≤ 10 keV) and the resonance harmonic is low (n = 0,1,2).
In the first subsection, we discuss the modeling of RF k∥ spectrum. In the second subsection, we use the cold plasma model to calculate wave properties. In the third and fourth subsections, we use further approximations to give analytical formulas for the properties of LHW and ECW. This leads to a simplified description of LHCD and ECCD and allows us to compare our models and results with other codes.
We consider the two-fluids description of a non relativistic plasma in a constant magnetic field
B0 = B0 . In a continuous homogeneous linear medium, a Fourier component Eb
. In a continuous homogeneous linear medium, a Fourier component Eb verifies
the wave equation [?]
verifies
the wave equation [?]
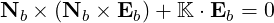 | (D.2) |
or equivalently
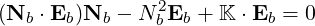 | (D.3) |
where Nb = ckb∕ωb is the wave refractive index and K is the dielectric tensor. This equation can be expressed in tensorial form as
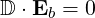 | (D.4) |
where the dispersion tensor is
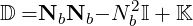 | (D.5) |
By evaluating the susceptibilities in the cold plasma limit, the following dielectric tensor is
obtained [?] in the frame 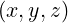 :
:
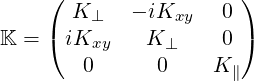 | (D.6) |
whose elements in a plasma made of species s are given by
| K⊥ | = 1 -∑
s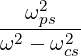 | ||
| K∥ | = 1 -∑
s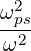 | ||
| Kxy | = -∑
s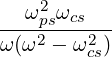 | (D.7) |
where
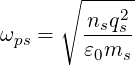 | (D.8) |
is the plasma frequency and
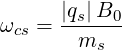 | (D.9) |
the cyclotron frequency for the species s.
In order to have a non-trivial solution to the wave equation, the dispersion relation must therefore be satisfied:
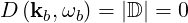 | (D.10) |
The axis 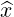 is chosen such that
is chosen such that
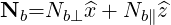 | (D.11) |
Taking the parallel component Nb∥ as given, (D.10) lead to the following equation for Nb⊥
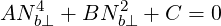 | (D.12) |
with
| A | = K⊥ | (D.13) |
| B | = 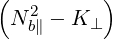 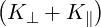 + Kxy2 + Kxy2 | (D.14) |
| C | = K∥![[ ( )2 ]
N 2b∥ - K⊥ - K2xy](NoticeDKE5162x.png) | (D.15) |
or equivalently
| A | = K⊥ | (D.16) |
| B | = 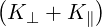 Nb∥2 - Nb∥2 -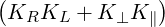 | (D.17) |
| C | = Kb∥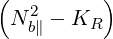 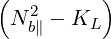 | (D.18) |
with
| KR | = K⊥ + Kxy | (D.19) |
| KL | = K⊥- Kxy | (D.20) |
We find the expression for Nb⊥ as a function of Nb∥ and ω:
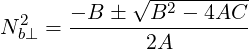 | (D.21) |
We see immediately that the resonances occur for A = 0, that is,
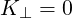 | (D.22) |
and that cut-offs occur for C = 0, that is,
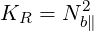 | (D.23) |
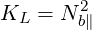 | (D.24) |
or
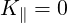 | (D.25) |
Once Nb⊥ has been evaluated, the components of the polarization of the electric field are simply given as the eigenvector of the wave equation (D.4)
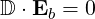 | (D.26) |
The relation between power flux and electric field was described using the vector Φb defined in (4.284)
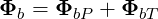 | (D.27) |
with (4.287)
![*
ΦbP = Re [Nb - (Nb ⋅eb)eb]](NoticeDKE5174x.png) | (D.28) |
and (4.286)
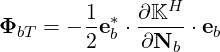 | (D.29) |
In the cold plasma model, the dielectric tensor K is independent of Nb and the contribution ΦbT , from the coherent motion of particles, vanishes.
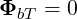 | (D.30) |
It is usually a very good approximation to neglect this kinetic power flux, even for quasi-electrostatic waves like Lower-Hybrid waves (See D.2.7).
The cold plasma model gives expressions (D.21), (D.26) and (D.28) for the calculation of N⊥, eb and Φb respectively. These formulas can be generally used for the calculation of the diffusion coefficient in LHCD and ECCD.