The tail part of the distribution function can be expressed in the simple form
where H
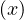is the usual Heaviside function while Θ∥f, Θ∥b and Θ⊥ are respectively
the parallel forward, backward and perpendicular pseudo-temperatures normalized to
mec2. They are considered as pseudo-temperatures, since they do not correspond to a
thermodynamic equilibrium for which the electron temperature Te has a true
physical meaning, i.e. the mean thermal velocity. They are introduced as simple
parameters to characterize the lack of symmetry around a given direction. Here, the
parallel component is expressed as
 | (36) |
where 
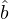is the unitary vector on the magnetic field line. Conversely, p⊥ is defined as
p2 = p∥2 + p⊥2. The distribution function f3T is also normalized to unity. Let pmin
being the momentum value corresponding to the intersection of f3T with fM, and
pmax, the upper limit above which it is zero.
 | (37) |
The presence of the Heaviside functions makes the calculation of the coefficient α3T non trivial. In the limits limpmin→0f3T and limpmax→+∞f3T, the parallel and perpendicular dynamics are decoupled, and an analytical expression may be derived. Indeed, In this case,
and a simple integration gives
 | (39) |
while
 | (40) |
Therefore, it is straightforward to find that
 | (41) |
and for the Maxwellian case Θ∥f = Θ∥b = Θ⊥ = Θ, one recovers well the relation
 | (42) |
Considering the reference to the thermal value pth† , defining p∥ = p∥pth† and p⊥ = p⊥pth†, as well as for the temperatures, one finds
using the identity for the Heaviside function
 | (44) |
and the fact that pth† > 0. The modified normalized coefficient is immediately
 | (45) |
