
The thermal distribution function is expressed in its general relativistic form
 | (2) |
where Θ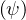 = Te
= Te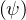 ∕mec2 is the ratio of the local electron temperature Te
∕mec2 is the ratio of the local electron temperature Te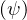 to
the electron rest mass energy mec2 while the relativistic Lorentz correction factor is
defined as γ2 = p2 + 1. Here, ξ is the cosine of the pitch angle. By symmetry, the
Maxwellian distribution function is independant of ξ. By definition, fM is
normalized to unity in the interval p ∈
to
the electron rest mass energy mec2 while the relativistic Lorentz correction factor is
defined as γ2 = p2 + 1. Here, ξ is the cosine of the pitch angle. By symmetry, the
Maxwellian distribution function is independant of ξ. By definition, fM is
normalized to unity in the interval p ∈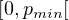 , where pmin is a given upper
cut-off limit for the Maxwellian. The parameter αM is then given by the
integral
, where pmin is a given upper
cut-off limit for the Maxwellian. The parameter αM is then given by the
integral
 | (3) |
Recalling that γdγ = pdp,
 | (4) |
where
 | (5) |
By integrating by parts
and in the limit pmin → +∞,
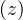 is the modified Bessel function of order 2.
is the modified Bessel function of order 2.
For Θ ≪ 1, using the large argument asymptotic development
 | (9) |
the usual expression keeping the first in the expansion
is well recovered and
 | (12) |
In the LUKE code, the momentum p here expressed in relativistic units mec is normalized to the thermal reference value pth† = mevth†,
 | (13) |
and consequently
 | (14) |
since thermal electrons are only weakly relativistic. The well known relativistic Lorentz correction factor γ is then simply given by the relation
 | (15) |
and in the non-relativistic limit, i.e. the condition p2βth†2 ≪ 1 or γ ≈ 1 holds.
Since in relativistic units, the total energy is linked to the relativistic momentum by the expression,
 | (16) |
it is straightforward to express the kinetic energy Ec as a function of p in units of electron rest mass energy mec2
 | (17) |
Finally, concerning the normalization of the electron velocity v, one has

 | (21) |
or
 | (22) |
with
 | (23) |
Consequently, the non-relativistic expression of fM is only valid when γ ≃ 1, or in an equivalent form
 | (24) |
Since p may be as large as 30 in numerical calculations, in order to correctly describe momentum dynamics of the fastest electrons, it results that
 | (25) |
or
 | (26) |
since βth† = 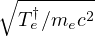 and Θ† = Te†∕mec2. Therefore, in a thermonuclear plasma,
one must always consider the relativistic form of the Maxwellian distribution
function. In addition, considering the asymptotic limit of K2 for large arguments
(??), the condition is
and Θ† = Te†∕mec2. Therefore, in a thermonuclear plasma,
one must always consider the relativistic form of the Maxwellian distribution
function. In addition, considering the asymptotic limit of K2 for large arguments
(??), the condition is
 | (27) |
or

which is always satisfied, since Te† never exceeds a few ten keV in tokamak plasmas. This means that the approximate formulation of f is fully valid.
In normalized units,

 | (30) |
since pth† = βth†, with
 | (31) |
and the modified normalisation coefficient becomes
 | (32) |
The Maxwellian distribution function be expressed in an alternative form, useful for calculating interpolation between full and half-grids,
 | (33) |
One can then easily cross-check that
 | (34) |
is well recovered.