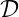
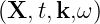 = 0 along the ray trajectory. Therefore, at all points along the ray trajectory, the
condition
= 0 along the ray trajectory. Therefore, at all points along the ray trajectory, the
condition
Ray equations in a plasma slowly varying in space and time are defined by the condition (??)
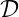
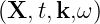 = 0 along the ray trajectory. Therefore, at all points along the ray trajectory, the
condition
= 0 along the ray trajectory. Therefore, at all points along the ray trajectory, the
condition
 | (25) |
must be satisfied. Let define τ a dimensionless parameter, which is a measure of distance along the trajectory. Then (??) can be rewritten as
 | (26) |
where Ẋ =dX∕dτ, 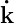 =dk∕dτ, ṫ=dt∕dτ and
=dk∕dτ, ṫ=dt∕dτ and 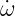 = dω∕dτ. The wave vector k is expressed in
coordinates that are canonically conjugate to those of the position vector X
= dω∕dτ. The wave vector k is expressed in
coordinates that are canonically conjugate to those of the position vector X
 | (27) |
where 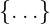 is Poisson bracket, δij is the Kronecker delta symbol, Xi and kj are the coordinate
of X and k respectively. The frequency ω and the time t being also canonically conjugate, the
relations
is Poisson bracket, δij is the Kronecker delta symbol, Xi and kj are the coordinate
of X and k respectively. The frequency ω and the time t being also canonically conjugate, the
relations
 | (28) |
result from the Hamiltonian nature of 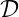 , and Eq. ?? is automatically satisfied. These four
equations are therefore the ray equations. From the first and the third equations,
, and Eq. ?? is automatically satisfied. These four
equations are therefore the ray equations. From the first and the third equations,
 | (29) |
meaning that the ray is directed along the group velocity vg and thus indicates the direction of
energy flow since vg∥S [13]. In a constant plasma ∂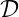 ∕∂t = 0 and ω is a constant of the ray
dynamics. The time t is considered as the evolution parameter of the ray and the two remaining
equations are
∕∂t = 0 and ω is a constant of the ray
dynamics. The time t is considered as the evolution parameter of the ray and the two remaining
equations are
 | (30) |
which are the usual forms found in the literature. However, one may also keep the simple form
 | (31) |
if the determination of the group velocity from ∂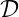 ∕∂ω is not required. This reduces the number
of derivative to calculate.
∕∂ω is not required. This reduces the number
of derivative to calculate.
We define Y the 8-dimension vector that represents the phase-space coordinates
 | (32) |
The ray equations (??-??) require to evaluate the derivatives of the dispersion relation (??) with respect to the coordinates of Y, explicitly
 | (33) |
Since Xs = Xs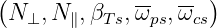 ,
,
In this equation the derivatives of the susceptibility tensor depend upon the plasma dispersion model (i.e. cold, kinetic, etc) while the derivatives with respect to Y are function of the equilibrium and the coordinate system.