4.1 Flux coordinate system
In an axisymmetric toroidal plasma we define the coordinate system 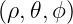 where θ is the
poloidal angle measured counterclockwise from the horizontal outboard midplane, ϕ is the
toroidal angle measured clockwise from the top, and ρ is a radial coordinate that varies between
0 on the axis and 1 at the plasma edge. The coordinate ρ = ρ
where θ is the
poloidal angle measured counterclockwise from the horizontal outboard midplane, ϕ is the
toroidal angle measured clockwise from the top, and ρ is a radial coordinate that varies between
0 on the axis and 1 at the plasma edge. The coordinate ρ = ρ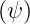 must be a flux function, i.e. a
monotonic function of the poloidal magnetic flux coordinate ψ defined by the following
expression of the magnetic field [9]
must be a flux function, i.e. a
monotonic function of the poloidal magnetic flux coordinate ψ defined by the following
expression of the magnetic field [9]
 | (35) |
which can be rewritten as
 | (36) |
where σB is the sign of Bϕ and σI is the sign of Iϕ. BT = 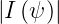 ∕R and BP =
∕R and BP = 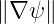 ∕R are
definite positive and ŝ =
∕R are
definite positive and ŝ = 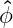 ×
×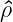 with ∇ρ =
with ∇ρ = 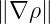
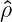 such that ŝ is orientated counter-clockwise in
the poloidal plane.
such that ŝ is orientated counter-clockwise in
the poloidal plane.
In the 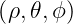 coordinate system the covariant coordinates of the wave vector k
are
coordinate system the covariant coordinates of the wave vector k
are
 | (37) |
The Poisson matrix of canonically conjugate X and k is
 | (38) |
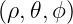 where θ is the
poloidal angle measured counterclockwise from the horizontal outboard midplane, ϕ is the
toroidal angle measured clockwise from the top, and ρ is a radial coordinate that varies between
0 on the axis and 1 at the plasma edge. The coordinate ρ = ρ
where θ is the
poloidal angle measured counterclockwise from the horizontal outboard midplane, ϕ is the
toroidal angle measured clockwise from the top, and ρ is a radial coordinate that varies between
0 on the axis and 1 at the plasma edge. The coordinate ρ = ρ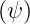 must be a flux function, i.e. a
monotonic function of the poloidal magnetic flux coordinate ψ defined by the following
expression of the magnetic field [9]
must be a flux function, i.e. a
monotonic function of the poloidal magnetic flux coordinate ψ defined by the following
expression of the magnetic field [9]


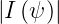
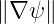
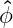
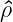 with
with 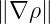
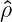 such that
such that 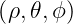 coordinate system the covariant coordinates of the wave vector
coordinate system the covariant coordinates of the wave vector 
