2.6 Weak damping approximation

Assuming that ω and N_∥ are given real quantities, (??) generally leads to a complex N_⊥ = N_⊥r + iN_⊥i. Meanwhile, the dispersion tensor D can be generally decomposed as D = D^H + iD^A where D^H = (D + D^†)∕2 and D^A = (D - D^†)∕2i are the hermitian and antihermitian parts of D, respectively. In this work, the weak damping approximation is considered, which is valid if |D_ij^A|≪|D_ij^H|. In that case, it can be shown [12] that |N_⊥i|≪|N_⊥r| and N_⊥r can be determined from solving the approximate wave equation

(19)

with dispersion relation

(20)

In this approximation, the time-averaged densities of energy flow S and dissipated power P can be obtained from

(21)

Note that the imaginary part of the wave vector can be calculated using

(22)

which yields the ray damping. From here on in this paper, k and N will refer to the zero-order, real solution of (??), and the dispersion relation 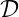to the hermitian part 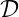^H.