
In order to obtain non-trivial solutions to the Eq. ??, the determinant of the dispersion tensor must be zero,
 | (18) |
which defines the dispersion relation. This relation gives the local electromagnetic
eigenmodes that can be excited independently in the homogenous plasma. By cylindrical
symmetry about the direction of the magnetic field 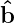 = B0∕B0,
= B0∕B0, 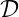 depends only upon the
components of N parallel and perpendicular to the magnetic field, defined respectively as
N∥ = N ⋅
depends only upon the
components of N parallel and perpendicular to the magnetic field, defined respectively as
N∥ = N ⋅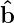 and N⊥ =
and N⊥ = 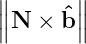 . Thus, the dispersion relation (??) can be solved for either
ω
. Thus, the dispersion relation (??) can be solved for either
ω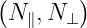 , N∥
, N∥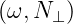 or N⊥
or N⊥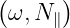 . The polarization of any eigenmode resulting from
equation (??) is determined by the corresponding eigenvector of the wave equation
(??).
. The polarization of any eigenmode resulting from
equation (??) is determined by the corresponding eigenvector of the wave equation
(??).
Explicit expressions of the dispersion relation are given in Appendix A1.