Combining the last two equations in (??) with (??) leads to the linear wave equation
|
| (9) |
where
 | (10) |
is the permittivity tensor,
 | (11) |
is the susceptibility tensor and I is the unit tensor.
Introducing the index of refraction
 | (12) |
the wave equation becomes
 | (13) |
or equivalently
 | (14) |
where D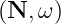
 | (15) |
is the dispersion tensor. The susceptibility X is the sum of contributions from all species
 | (16) |
In the case where the distribution function of the species s is a Maxwellian, Xs depends upon
the following non-dimensional parameters : the refractive index N, the thermal velocity
normalized to the speed of light βTs = vTs∕c where vTs =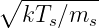 
, and the ratios ωps = ωps∕ω
and ωcs = ωcs∕ω of the plasma frequency ωps = 
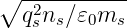and the cyclotron frequency
ωcs = qsB0∕ms to the wave frequency ω. Therefore the dispersion tensor may be expressed in
the general form
 | (17) |