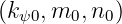 at the position
at the position 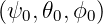 , the problem is to evaluate
, the problem is to evaluate
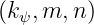 and
and 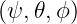 at all values of the time parameter t.
at all values of the time parameter t.
Relations (??-??) form a system of first order coupled differential equations. Knowing the initial
wave characteristics 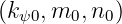 at the position
at the position 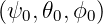 , the problem is to evaluate
, the problem is to evaluate
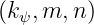 and
and 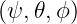 at all values of the time parameter t.
at all values of the time parameter t.
There are several algorithms for solving this initial value problem,
minimizing propagation of the numerical error. One of the most popular is
the Runge-Kutta algorithm which belongs to the Euler-Cauchy algorithm
family3.
The procedure consists in solving the differential equations of the type y′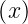 = f
= f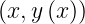 by an
iterative method, with the recurrence rule
by an
iterative method, with the recurrence rule
 | (76) |
and the initial condition y0 = y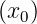 .
.
A solution of the following form is seeked
 | (77) |
so that no numerical derivatives need to be calculated. From a Taylor series expansion of y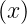 up to the second order, one obtains
up to the second order, one obtains
where
 | (80) |
A similar expansion gives
 | (81) |
Thus, up to the 2nd order, φ becomes
 | (82) |
so that
In order to obtain a second order accurate calculation, the coefficients must satisfy the relations
 | (84) |
which implies
 | (85) |
The solution is finally
 | (86) |
where the case α = 1∕2 corresponds to the Eun’s algorithm, while α = 1 is corresponding to the modified Euler’s algorithm.
A second order Runge-Kutta algorithm then corresponds to the following procedure,
 | (87) |
The parameter α is chosen depending upon the studied problem, and parameter h, which must be small, may be adjusted at each iteration step, as function of the local curvature of the ray path. This is the adaptative Runge-Kutta method, widely used for solving this type of problem.
This procedure, which has been highlighted for order 2, may be expanded in a similar manner to higher orders. Detailed calculations can be found in the literature [11].
In the ray-tracing code, a sixth order adaptative Runge-Kutta integration method is used.
The numerical accuracy obtained with this method is very satisfactory, and the condition
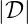 ≤ 10-10 is usually obtained along the ray path, despite a sudden increase in
≤ 10-10 is usually obtained along the ray path, despite a sudden increase in 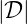 sometimes
observed near the cold/fast wave mode conversion.
sometimes
observed near the cold/fast wave mode conversion.