5.1 Magnetic equilibrium interpolation
Since magnetic equilibrium codes give field components on a discrete two dimensional grid mesh
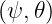 , it is necessary to perform a numerical interpolation at the ray location. This procedure
must be fast and very accurate an including first and second derivatives upon which the
ray-tracing is very sensitive. Indeed, coarse interpolation may lead to large cumulative errors
along the ray path and, ultimately, a wrong trajectory.
, it is necessary to perform a numerical interpolation at the ray location. This procedure
must be fast and very accurate an including first and second derivatives upon which the
ray-tracing is very sensitive. Indeed, coarse interpolation may lead to large cumulative errors
along the ray path and, ultimately, a wrong trajectory.
Among several methods,
the combination of Fourier expansion and spline interpolation is chosen, taking into account of
the periodic nature of the poloidal angle θ. Any function g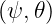 is expressed as a Fourier
sum
is expressed as a Fourier
sum
 | (71) |
where N ≤ Nθ∕2 according to the Shannon theorem where Nθ is the number of discrete
poloidal values. The Fourier an(c,s)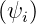 coefficients are determined on each discrete magnetic
flux surface ψi in order to satisfy
coefficients are determined on each discrete magnetic
flux surface ψi in order to satisfy
 | (72) |
then the coefficients an(c,s)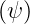 at any radial position ψ
i < ψ < ψi+1 are obtained using a usual
cubic spline interpolation
at any radial position ψ
i < ψ < ψi+1 are obtained using a usual
cubic spline interpolation
 | (73) |
the 3rd order polynomial coefficients being calculated so that at all nodes ψi, an(c,s)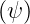 is
continuous, as well as its first and second derivatives.
is
continuous, as well as its first and second derivatives.
Then the derivatives at any 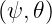 position are obtained from the relations
position are obtained from the relations
 | (74) |
where
 | (75) |
Note that for density and temperature profiles only a cubic spline interpolation is performed,
since these parameters are function of ψ only. With typically 65 poloidal angle values and 101
radial discrete positions, the relative accuracy of the magnetic equilibrium is of the order of
10-4 approximately. Larger numerical errors may occur near a X-point, where the local
curvature radius of all magnetic flux surfaces becomes very small. In that case and if a more
detailed interpolated magnetic reconstruction is required, more poloidal points must be used in
this region of the plasma, keeping the same total number of poloidal values on a non-uniform
grid. When some smoothing is needed, it is always possible to use less coefficients in the Fourier
expansion series.
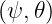 , it is necessary to perform a numerical interpolation at the ray location. This procedure
must be fast and very accurate an including first and second derivatives upon which the
ray-tracing is very sensitive. Indeed, coarse interpolation may lead to large cumulative errors
along the ray path and, ultimately, a wrong trajectory.
, it is necessary to perform a numerical interpolation at the ray location. This procedure
must be fast and very accurate an including first and second derivatives upon which the
ray-tracing is very sensitive. Indeed, coarse interpolation may lead to large cumulative errors
along the ray path and, ultimately, a wrong trajectory.
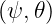 is expressed as a Fourier
sum
is expressed as a Fourier
sum

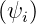 coefficients are determined on each discrete magnetic
flux surface
coefficients are determined on each discrete magnetic
flux surface 
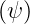 at any radial position
at any radial position 
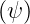 is
continuous, as well as its first and second derivatives.
is
continuous, as well as its first and second derivatives.
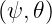 position are obtained from the relations
position are obtained from the relations

