Reverse field pinch plasma

E.4 Reverse field pinch plasma

E.4.1 Equilibrium

Figure 15: Poloidal projection of the ray trajectory in the slow mode (RFP).

Figure 16: Toroidal projection of the ray trajectory in the slow mode (RFP).

Figure 17: Parallel refractive index or refraction along the ray trajectory (RFP).

Figure 18: Dispersion relation along the ray trajectory (RFP).

In Reverse Field Pinch, the plasma evolves to a quasi-stationary magnetic equilibrium close to the force free minimum energy states described by Taylor [17]. The fully relaxed Taylor states are characterized by

\text{[math]}

(194)

with

\text{[math]}

(195)

constant throughout the plasma. A usual simplified approach is to consider a circular concentric toroidal plasma such that

\text{[math]}

(196)

with the following equilibrium parameters⁷

\text{[math]}

(197)

From Eq. ??, considering a constant λ value,

which leads to two coupled equations

Inserting Eq.?? into Eq.?? in order to eliminate B_θ, one finds the equation for B_ϕ

\text{[math]}

(203)

which can be developed as

\text{[math]}

(204)

Assuming a low inverse aspect ratio limit, and neglecting all terms higher than (a_p∕R_p)²,

\text{[math]}

(205)

and

\text{[math]}

(206)

which is a Bessel equation whose solution is

\text{[math]}

(207)

Reporting this equation in Eq.??, and using the derivative identity for Bessel functions of order m,

\text{[math]}

(208)

one finds

\text{[math]}

(209)

From the determination of B_ϕ and B_θ, it turns finally out that 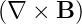(∇ × B) _r = 0, and therefore Eq.?? is well satisfied.

For the ray-tracing calculations, the magnetic equilibrium is chosen so that λa_p = ^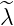
λ = 2.2. From these definition, up to the same order, the safety factor is

\text{[math]}

(210)

For the cold plasma model, the electron density profile is

\text{[math]}

(211)

with

\text{[math]}

(212)

while the main plasma gas is Deuterium. Calculations are performed with a uniform effective charge Z_eff = 2, using the fully stripped single impurity model, with Carbon.

E.4.2 Wave initial conditions

The ray is launched in the slow mode from the position

\text{[math]}

(213)

with the spectral properties

\text{[math]}

(214)

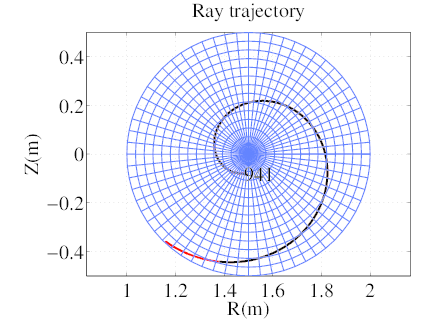
It is worth noting that since at the plasma edge of a RFP, magnetic field lines are almost in the poloidal direction, the toroidal wave number n₀ must be zero, instead of m₀ usually used for tokamaks, where edge magnetic field lines are almost aligned toroidally. Because of the axisymmetry, n remains equal to zero along the ray propagation. Nevertheless, rays may propagate toroidally.

E.4.3 Results

The results are shown in figures 15-18. A strong poloidal upshift is observed as the LH wave propagates, and as found by previous publications, the ray does a spiral around the magnetic axis. Even if the magnetic equilibrium strongly differs from the usual tokamak one, the dispersion relation is well fulfilled along the ray path.

[prev] [prev-tail] [front] [up]