In vacuum, electromagnetic waves trajectories are straight lines, which offers an interesting benchmarking case for the curvilinear coordinate system used with C3PO ray-tracing. It is enforced that at ψ = ψa the wave is reflected like in a mirror, so that the ray remains confined in the machine. Circular concentric poloidal magnetic flux surfaces are considered with
 | (180) |
and the poloidal magnetic field is considered to be created by a virtual toroidal current Ip of 1.0 MA and a parabolic safety factor profile of the form
 | (181) |
with qmin = 1 and qmax obtained from Ampère’s law.
Since rays are straight lines, it is possible to calculate the exact rays trajectories
from geometrical arguments. Since 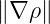 = 1, the initial value of the wave vector is
k0 = kρ0
= 1, the initial value of the wave vector is
k0 = kρ0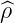 + kθ0
+ kθ0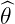 + kϕ0
+ kϕ0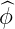 with kθ0 = m0ap∕ρ0 and kϕ = n0ap∕R0. k0 is expressed in cartesian
coordinates using the relation k0cartesian = M
cc
with kθ0 = m0ap∕ρ0 and kϕ = n0ap∕R0. k0 is expressed in cartesian
coordinates using the relation k0cartesian = M
cc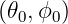 ⋅ k0curvilinear where
⋅ k0curvilinear where
 | (182) |
The initial position at launch in the cartesian coordinates 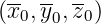 normalized to ap is given
by the relations
normalized to ap is given
by the relations
 | (183) |
where 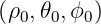 are initial curvilinear coordinates. Since the ray is a straight line, its position
is given by the parametric equation
are initial curvilinear coordinates. Since the ray is a straight line, its position
is given by the parametric equation
 | (184) |
where s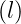 is the ray length starting from s
is the ray length starting from s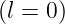 = 0 at
= 0 at 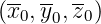 .Once
.Once 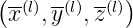 known, it is possible to determine back
known, it is possible to determine back 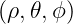 by inverting (??). From the determination of
by inverting (??). From the determination of
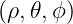 , it is possible to evaluate klcurvilinearat all positions, using k
lcartesian = k
0cartesian
and
, it is possible to evaluate klcurvilinearat all positions, using k
lcartesian = k
0cartesian
and
 | (185) |
Then m = k
θ
= k
θ ρ
ρ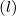 ∕a
p and n
∕a
p and n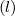 = k
ϕ
= k
ϕ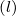 R
R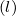 ∕a
p
∕a
p
In order to keep the ray inside the toroidal chamber, a specular reflection is enforced at ψa.If
the condition ρ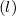 > 1 is encountered, then the new direction of the ray k
0
> 1 is encountered, then the new direction of the ray k
0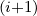 cartesian of the i + 1
ray segment is deduced from k0
cartesian of the i + 1
ray segment is deduced from k0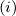 cartesian according to the conditions
cartesian according to the conditions
where 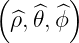 are used at the increment
are used at the increment 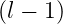 . It corresponds to the relation
. It corresponds to the relation
 | (189) |
with
 | (190) |
and
 | (191) |
In the example here given, the ray is launched from the position
 | (192) |
with spectral properties
 | (193) |
so that the wave can propagate into vacuum region.
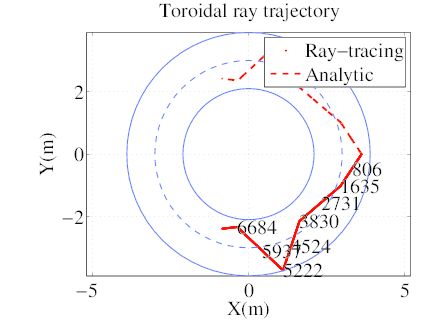
As expected, ray trajectory is made of pieces of straight lines, which can be easily shown from the toroidal projection in Fig 13. Because of the toroidal topology, the poloidal projection in Fig. 14 does not give straight lines. This result highlights the fact that it is very difficult to have a correct picture of the ray path from this type of representation. Comparison with simple geometrical optics is excellent.